Language accepted by Turing machine

The Turing machine accepts all the language even though they are recursively enumerable. Recursive means repeating the same set of rules for any number of times and enumerable means a list of elements. The TM also accepts the computable functions, such as addition, multiplication, subtraction, division, power function, and many more.

Example:

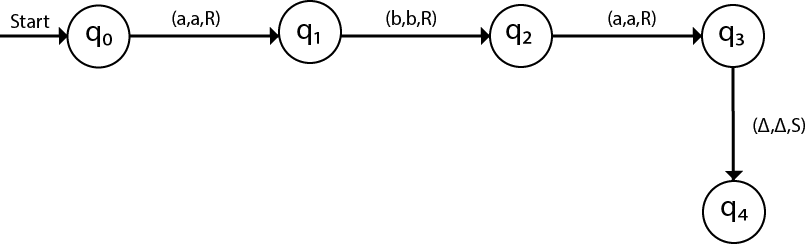
Construct a Turing machine which accepts the language of aba over ∑ = {a, b}.

Solution:

We will assume that on input tape the string 'aba' is placed like this:

The tape head will read out the sequence up to the Δ characters. If the tape head is readout 'aba' string then TM will halt after reading Δ.

Now, we will see how this turing machine will work for aba. Initially, state is q0 and head points to a as:

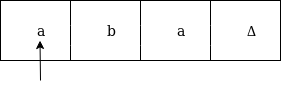
The move will be δ(q0, a) = δ(q1, A, R) which means it will go to state q1, replaced a by A and head will move to right as:

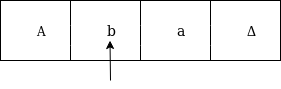
The move will be δ(q1, b) = δ(q2, B, R) which means it will go to state q2, replaced b by B and head will move to right as:

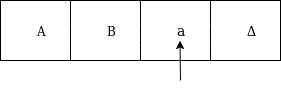
The move will be δ(q2, a) = δ(q3, A, R) which means it will go to state q3, replaced a by A and head will move to right as:

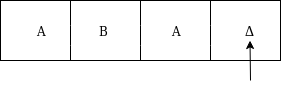
The move δ(q3, Δ) = (q4, Δ, S) which means it will go to state q4 which is the HALT state and HALT state is always an accept state for any TM.

The same TM can be represented by Transition Table:

States	a	b	Δ
q0	(q1, A, R)	–	–
q1	–	(q2, B, R)	–
q2	(q3, A, R)	–	–
q3	–	–	(q4, Δ, S)
q4	–	–	–

The same TM can be represented by Transition Diagram: