Examples of TM

Turing Machine for anbn where n>=1

Turing Machine for anbncnwhere n>=1

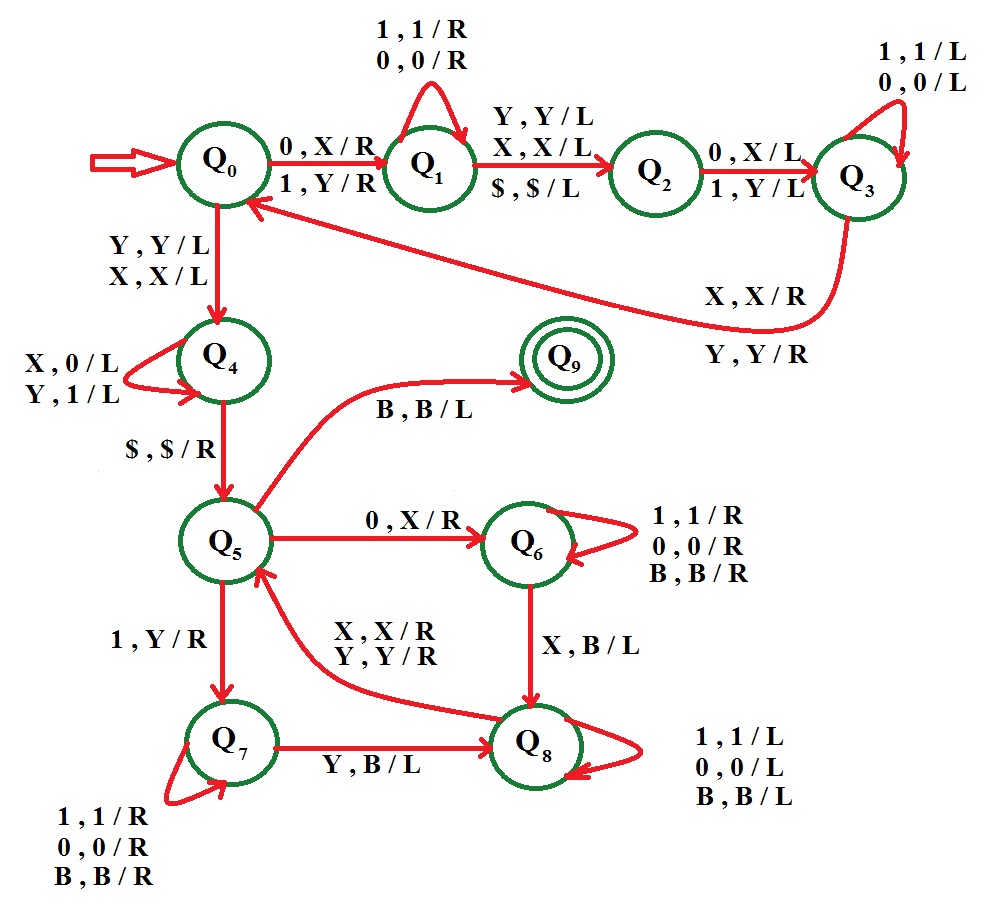
Example: Construct a Turing Machine for language L = {ww | w ∈ {0,1}}

The language L = {ww | w ∈ {0, 1}} tells that every string of 0’s and 1’s which is followed by itself falls under this language. The logic for solving this problem can be divided into 2 parts:

1. Finding the mid point of the string 
2. After we have found the mid point we match the symbols

Example – Lets understand it with the help of an example. Lets string 1 0 1 1 0 1, so w = 1 0 1 and string is of form (ww). 

The first thing that we do is to find the midpoint. For this, we convert 1 in the beginning into Y and move right till the end of the string. Here we convert 1 into y. 

Now our string would look like Y 0 1 1 0 Y. Now move left till, find a X or Y. When we do so, convert the 0 or 1 right of it to X or Y respectively and then do the same on the right end. Now our string would look like Y X 1 1 X Y. Thereafter, convert these 1’s also and finally it would look like Y X Y Y X Y. 

At this point, you have achieved the first objective which was to find the midpoint. Now convert all X and Y on the left of midpoint into 0 and 1 respectively, so string becomes 1 0 1 Y X Y. Now, convert the 1 into Y and move right till, find Y in the beginning of the right part of the string and convert this Y into a blank (denoted by B). Now string looks like Y 0 1 B X Y. 

Similarly, apply this on 0 and x followed by 1 and Y. After this string looks like Y X Y B B B. Now that you have no 0 and 1 and all X and Y on the right part of the string are converted into blanks so our string will be accepted. 

Assumption: We will replace 0 by X and 1 by Y. 

Approach Used – 

The first thing is to find the midpoint of the string, convert a 0 or 1 from the beginning of the string into X or Y respectively and a corresponding 0 or 1 into X or Y from the end of the string. After continuously doing it a point is reached when all 0’s and 1’s have been converted into X and Y respectively. At this point, you are on the midpoint of the string. So, our first objective is fulfilled. 

Now, convert all X’s and Y’s on the left of the midpoint into 0’s and 1’s. At this point the first half the string is in the form of 0 and 1. The second half of the string is in the form of X and Y. 

Now, start from the beginning of the string. If you have a 0 then convert it into X and move right till reaching the second half, here if we find X then convert it into a blank(B). Then traverse back till find an X or a Y. We convert the 0 or 1 on the right of it into X or Y respectively and correspondingly, convert its X or Y in the second half of string into a blank(B). 

Keep doing this till converted all symbols on the left part of the string into X and Y and all symbols on the right of string into blanks. If any one part is completely converted but still some symbols in the other half are left unchanged then the string will not be accepted. If you did not find an X or Y in the second half for a corresponding 0 or 1 respectively in the first half. Then also string will not be accepted. 

Examples: 

 

Input  : 1 1 0 0 1 1 0 0 
Output : Accepted

Input  : 1 0 1 1 1 0 1
Output : Not accepted

 

• Step-1: 
  If the symbol is 0 replace it by X and move right 
  If the symbol is 1 replace it by Y and move right, 
  Go to state Q1 and step 2 
  ——————————————— 
  If the symbol is X replace it by X and move left or 
  If the symbol is Y replace it by Y and move left, 
  Go to state Q4 and step 5 

   

• Step-2: 
  If the symbol is 0 replace it by 0 and move right, remain on the same state 
  If the symbol is 1 replace it by 1 and move right, remain on the same state 
  ——————————————— 
  If the symbol is X replace it by X and move left or 
  If the symbol is Y replace it by Y and move left or 
  If the symbol is $ replace it by $ and move left, Go to state Q2 and step 3 

   

• Step-3: 
  If symbol is 0 replace it by X and move left, or 
  If symbol is 1 replace it by Y and move left, 
  Go to state Q3 and step 4 

   

• Step-4: 
  If the symbol is 0 replace it by 0 and move left, remain on the same state 
  If the symbol is 1 replace it by 1 and move left, remain on the same state 
  ——————————————— 
  If the symbol is X replace it by X and move right or 
  If the symbol is Y replace it by Y and move right, 
  Go to state Q0 and step 1 

   

• Step-5: 
  If symbol is X replace it by X and move left or 
  If symbol is Y replace it by Y and move left 
  Go to state Q4 and step 6 

   

• Step-6: 
  If symbol is X replace it by 0 and move left, remain on same state 
  If symbol is Y replace it by 1 and move left, remain on same state 
  – – – – – – – – – — – – – – – – – – – — 
  If symbol is $ replace it by $ and move right 
  Go to state Q4 and step 7 

   

• Step-7: 
  If symbol is 0 replace it by X and move right, go to state Q6 and step 8 
  If symbol is 1 replace it by Y and move right, go to state Q7 and step 9 
  – – – – – – – – – — – – – – – – – – – — 
  If symbol is B replace it by B and move left, STRING ACCEPTED, GO TO FINAL STATE Q9 

   

• Step-8: 
  If symbol is 0 replace it by 0 and move right, remain on same state 
  If symbol is 1 replace it by 1 and move right, remain on same state 
  If symbol is B replace it by B and move right, remain on same state 
  – — – – – – – – – – – – – – – – – – – – 
  If symbol is X replace it by B and move left 
  Go to state Q8 and step 10 

   

• Step-9: 
   

If symbol is 0 replace it by 0 and move right, remain on same state 

If symbol is 1 replace it by 1 and move right, remain on same state 

If symbol is B replace it by B and move right, remain on same state 

– — – – – – – – – – – – – – – – – – – – 

If symbol is Y replace it by B and move left 

Go to state Q8 and step 10 

 

• Step-10: 
  If symbol is 0 replace it by 0 and move left, remain on same state 
  If symbol is 1 replace it by 1 and move left, remain on same state 
  If symbol is B replace it by B and move left, remain on same state 
  – — – – – – – – – – – – – – – – – – – – 
  If symbol is Y replace it by Y and move right or 
  If symbol is X replace it by X and move right 
  Go to state Q5 and step 7 
   

 

Example:

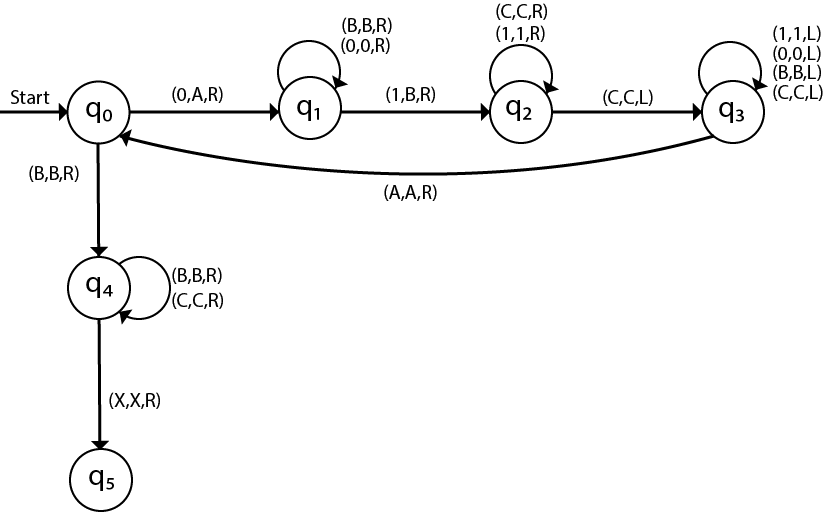
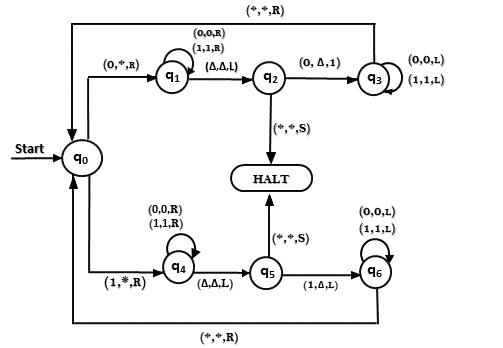
Construct a TM for the language L = {0ⁿ1ⁿ2ⁿ} where n≥1

Solution:

L = {0ⁿ1ⁿ2ⁿ | n≥1} represents language where we use only 3 character, i.e., 0, 1 and 2. In this, some number of 0's followed by an equal number of 1's and then followed by an equal number of 2's. Any type of string which falls in this category will be accepted by this language.

The simulation for 001122 can be shown as below:

Now, we will see how this Turing machine will work for 001122. Initially, state is q0 and head points to 0 as:

The move will be δ(q0, 0) = δ(q1, A, R) which means it will go to state q1, replaced 0 by A and head will move to the right as:

The move will be δ(q1, 0) = δ(q1, 0, R) which means it will not change any symbol, remain in the same state and move to the right as:

The move will be δ(q1, 1) = δ(q2, B, R) which means it will go to state q2, replaced 1 by B and head will move to right as:

The move will be δ(q2, 1) = δ(q2, 1, R) which means it will not change any symbol, remain in the same state and move to right as:

The move will be δ(q2, 2) = δ(q3, C, R) which means it will go to state q3, replaced 2 by C and head will move to right as:

Now move δ(q3, 2) = δ(q3, 2, L) and δ(q3, C) = δ(q3, C, L) and δ(q3, 1) = δ(q3, 1, L) and δ(q3, B) = δ(q3, B, L) and δ(q3, 0) = δ(q3, 0, L), and then move δ(q3, A) = δ(q0, A, R), it means will go to state q0, replaced A by A and head will move to right as:

The move will be δ(q0, 0) = δ(q1, A, R) which means it will go to state q1, replaced 0 by A, and head will move to right as:

The move will be δ(q1, B) = δ(q1, B, R) which means it will not change any symbol, remain in the same state and move to right as:

The move will be δ(q1, 1) = δ(q2, B, R) which means it will go to state q2, replaced 1 by B and head will move to right as:

The move will be δ(q2, C) = δ(q2, C, R) which means it will not change any symbol, remain in the same state and move to right as:

The move will be δ(q2, 2) = δ(q3, C, L) which means it will go to state q3, replaced 2 by C and head will move to left until we reached A as:

immediately before B is A that means all the 0's are market by A. So we will move right to ensure that no 1 or 2 is present. The move will be δ(q2, B) = (q4, B, R) which means it will go to state q4, will not change any symbol, and move to right as:

The move will be (q4, B) = δ(q4, B, R) and (q4, C) = δ(q4, C, R) which means it will not change any symbol, remain in the same state and move to right as:

The move δ(q4, X) = (q5, X, R) which means it will go to state q5 which is the HALT state and HALT state is always an accept state for any TM.

The same TM can be represented by Transition Diagram:

Example 2:

Construct a TM machine for checking the palindrome of the string of even length.

Solution:

Firstly we read the first symbol from the left and then we compare it with the first symbol from right to check whether it is the same.

Again we compare the second symbol from left with the second symbol from right. We repeat this process for all the symbols. If we found any symbol not matching, we cannot lead the machine to HALT state.

Suppose the string is ababbabaΔ. The simulation for ababbabaΔ can be shown as follows:

Now, we will see how this Turing machine will work for ababbabaΔ. Initially, state is q0 and head points to a as:

We will mark it by * and move to right end in search of a as:

We will move right up to Δ as:

We will move left and check if it is a:

It is 'a' so replace it by Δ and move left as:

Now move to left up to * as:

Move right and read it

Now convert b by * and move right as:

Move right up to Δ in search of b as:

Move left, if the symbol is b then convert it into Δ as:

Now move left until * as:

Replace a by * and move right up to Δ as:

We will move left and check if it is a, then replace it by Δ as:

It is 'a' so replace it by Δ as:

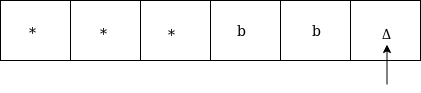
Now move left until *

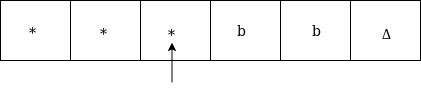
Now move right as:

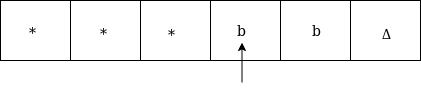
Replace b by * and move right up to Δ as:

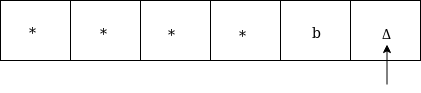
Move left, if the left symbol is b, replace it by Δ as:

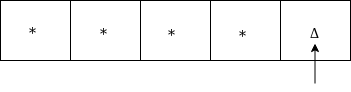
Move left till *

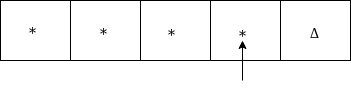
Move right and check whether it is Δ

Go to HALT state

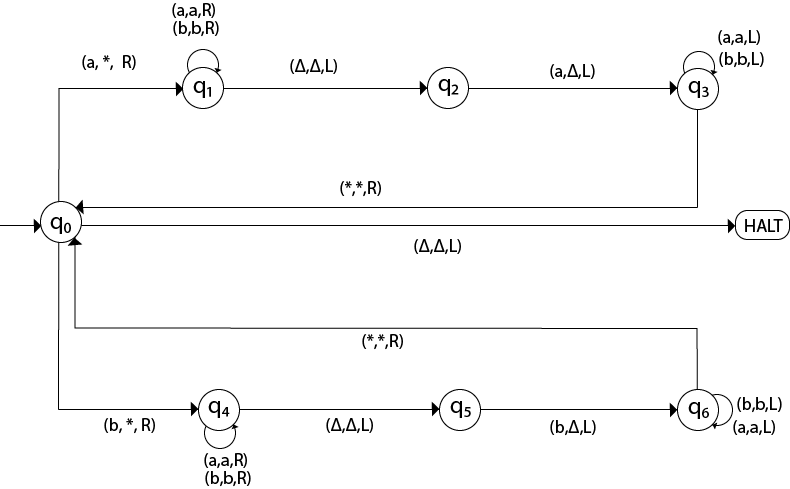
The same TM can be represented by Transition Diagram:

Example 3:

Construct a TM machine for checking the palindrome of the string of odd length.

Solution:

Firstly we read the first symbol from left and then we compare it with the first symbol from right to check whether it is the same.

Again we compare the second symbol from left with the second symbol from right. We repeat this process for all the symbols. If we found any symbol not matching, we lead the machine to HALT state.

Suppose the string is 00100Δ. The simulation for 00100Δ can be shown as follows:

Now, we will see how this Turing machine will work for 00100Δ. Initially, state is q0 and head points to 0 as:

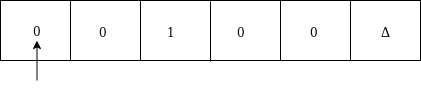
Now replace 0 by * and move right as:

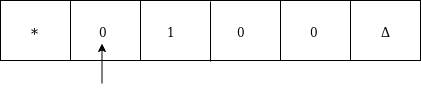
Move right up to Δ as:

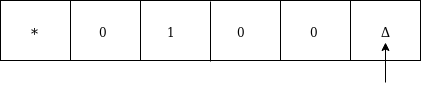
Move left and replace 0 by Δ and move left:

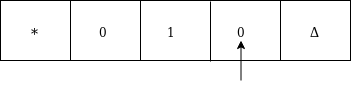
Now move left up to * as:

Move right, convert 0 by * and then move right as:

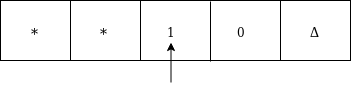
Moved right up to Δ

Move left and replace 0 by Δ as:

Move left till * as:

Move right and convert 1 to * as:

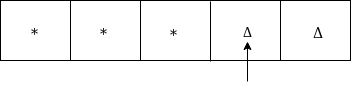
Move left

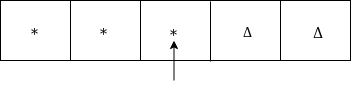
Since it is *, goto HALT state.

The same TM can be represented by Transition Diagram:

Example 4:

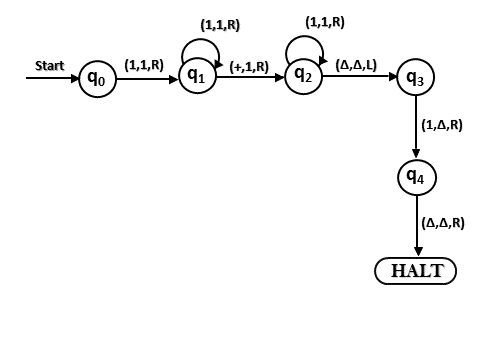
Construct TM for the addition function for the unary number system.

Solution:

The unary number is made up of only one character, i.e. The number 5 can be written in unary number system as 11111. In this TM, we are going to perform the addition of two unary numbers.

For example

2 + 3
i.e. 11 + 111 = 11111

If you observe this process of addition, you will find the resemblance with string concatenation function.

In this case, we simply replace + by 1 and move ahead right for searching end of the string we will convert last 1 to Δ.

Input: 3+2

The simulation for 111+11Δ can be shown as below:

Move right up to + sign as:

Convert + to 1 and move right as:

Now, move right

Again move right

Now Δ has encountered, so just move left as:

Convert 1 to Δ

Thus the tape now consists of the addition of two unary numbers.

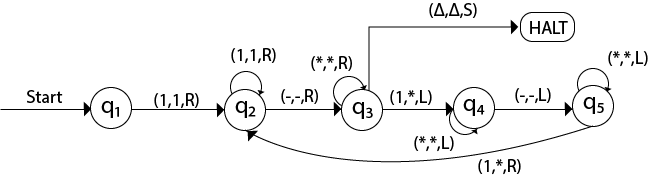
The TM will look like as follows:

Here, we are implementing the function of f(a + b) = c. We assume a and b both are non zero elements.

Example 5:

Construct a TM for subtraction of two unary numbers f(a-b) = c where a is always greater than b.

Solution: Here we have certain assumptions as the first number is greater than the second one. Let us assume that a = 3, b = 2, so the input tape will be:

We will move right to - symbol as perform reduction of a number of 1's from the first number. Let us look at the simulation for understanding the logic:

Move right up to - as:

Move right and convert 1 to * as:

Now move left

Again move left

Convert 1 to * and move right-hand

Now move right till 1

Convert 1 to * and move left

Convert 1 to * and move

Move right till Δ as:

Now we are in the HALT state.

Thus we get 1 on the input tape as the answer for f(3-2).

The Turing machine will look like this: