Reflection

It is a transformation which produces a mirror image of an object. The mirror image can be either about x-axis or y-axis. The object is rotated by180°.

Types of Reflection:

1. Reflection about the x-axis
2. Reflection about the y-axis
3. Reflection about an axis perpendicular to xy plane and passing through the origin
4. Reflection about line y=x

1. Reflection about x-axis: The object can be reflected about x-axis with the help of the following matrix

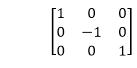
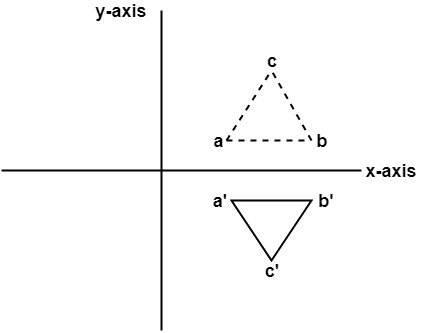
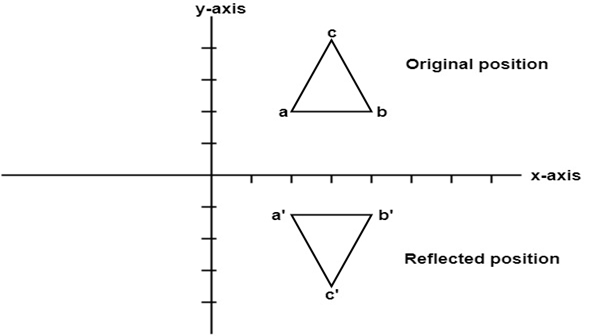
In this transformation value of x will remain same whereas the value of y will become negative. Following figures shows the reflection of the object axis. The object will lie another side of the x-axis.

2. Reflection about y-axis: The object can be reflected about y-axis with the help of following transformation matrix

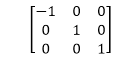
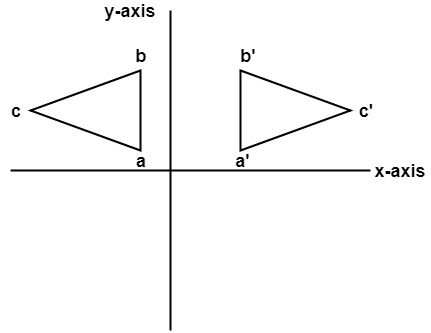
Here the values of x will be reversed, whereas the value of y will remain the same. The object will lie another side of the y-axis.

The following figure shows the reflection about the y-axis

3. Reflection about an axis perpendicular to xy plane and passing through origin:
In the matrix of this transformation is given below

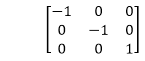
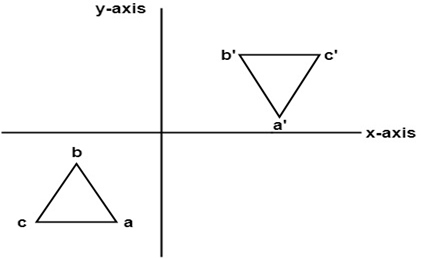
In this value of x and y both will be reversed. This is also called as half revolution about the origin.

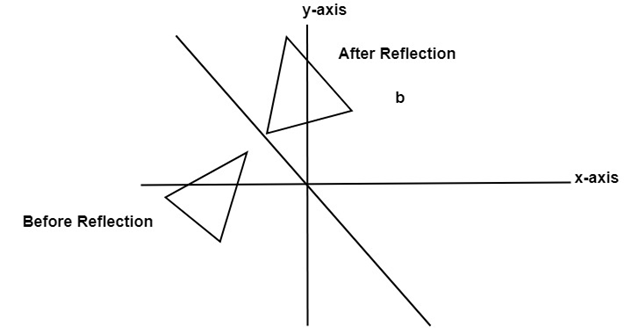
4. Reflection about line y=x: The object may be reflected about line y = x with the help of following transformation matrix

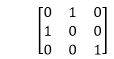
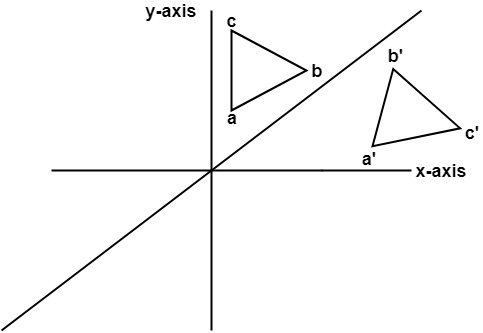
First of all, the object is rotated at 45°. The direction of rotation is clockwise. After it reflection is done concerning x-axis. The last step is the rotation of y=x back to its original position that is counterclockwise at 45°.

Example: A triangle ABC is given. The coordinates of A, B, C are given as

                    A (3 4)
                    B (6 4)
                    C (4 8)

Find reflected position of triangle i.e., to the x-axis.

Solution:

The a point coordinates after reflection

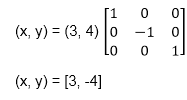
The b point coordinates after reflection

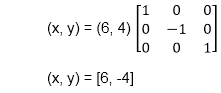
The coordinate of point c after reflection

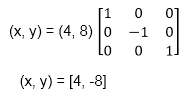
a (3, 4) becomes a¹ (3, -4)
b (6, 4) becomes b¹ (6, -4)
c (4, 8) becomes c¹ (4, -8)

Program to perform Mirror Reflection about a line:

#include <iostream.h>  
#include <conio.h>  
#include <graphics.h>  
#include <math.h>  
#include <stdlib.h>  
#define pi 3.14  
class arc  
{  
    float x[10],y[10],theta,ref[10][10],ang;  
           float p[10][10],p1[10][10],x1[10],y1[10],xm,ym;  
    int i,k,j,n;  
    public:  
    void get();  
    void cal ();  
    void map ();  
    void graph ();  
    void plot ();  
    void plot1();  
};  
void arc::get ()  
{  
    cout<<"\n ENTER ANGLE OF LINE INCLINATION AND Y INTERCEPT";  
    cin>> ang >> b;  
    cout <<"\n ENTER NO OF VERTICES";  
    cin >> n;  
    cout <<"\n ENTER";  
    for (i=0; i<n; i++)  
    {  
        cout<<"\n x["<<i<<"] and y["<<i<<"]";  
    }  
    theta =(ang * pi)/ 180;  
    ref [0] [0] = cos (2 * theta);  
    ref [0] [1] = sin (2 * theta);  
    ref [0] [2] = -b *sin (2 * theta);  
    ref [1] [0] = sin (2 * theta);  
    ref [1] [1] = -cos (2 * theta);  
    ref [1] [2] = b * (cos (2 * theta)+1);  
    ref [2] [0]=0;  
    ref [2] [1]=0;  
    ref [2] [2] = 1;  
}  
void arc :: cal ()  
{  
    for (i=0; i < n; i++)  
    {  
        p[0] [i] = x [i];  
        p [1] [i] = y [i];  
        p [2] [i] = 1;  
    }  
    for (i=0; i<3;i++)  
    {  
        for (j=0; j<n; j++)  
        {  
            p1 [i] [j]=0;  
            for (k=0;k<3; k++)  
        }  
        p1 [i] [j] + = ref [i] [k] * p [k] [j];  
             }  
for (i=0; i<n; i++)  
   {  
    x1 [i]=p1[0] [i];  
    y1 [i] = p1 [1] [i];  
    }  
}  
void arc :: map ()  
{  
    int gd = DETECT,gm;  
    initgraph (&gd, &gm, " ");  
            int errorcode = graphresult ();  
    /* an error occurred */  
    if (errorcode ! = grOK)      
    {  
        printf ("Graphics error: %s \n", grapherrormsg (errorcode));  
        printf ("Press any key to halt:");  
        getch ();  
        exit (1); /* terminate with an error code */  
    }  
}  
void arc :: graph ()  
{  
    xm=getmaxx ()/2;  
    ym=getmaxy ()/2;  
    line (xm, 0, xmm 2*ym);  
}  
void arc :: plot 1 ()  
{  
    for (i=0; i <n-1; i++)  
    {  
        circle (x1[i]+xm, (-y1[i]+ym), 2);  
        line (x1[i]+xm, (-y1[i]+ym), x1[i+1]+xm, (-y1[i+1]+ym));  
    }  
        line (x1[n-1)+xm, (-y1[n-1]+ym), x1[0]+xm, (-y1[0]+ym));  
        getch();  
}  
void arc :: plot ()  
{   
    for (i=0; i <n-1; i++)  
    {  
        circle (x1[i]+xm, (-y1[i]+ym, 2);  
        line (x1[i]+xm, (-y1[i]+ym), x[i+1]+xm, (-y1[i+1]+ym));  
    }  
        line (x[n-1]+xm, (-y1[n-1]+ym), x[0]+xm, (-y[0]+ym));  
        getch();  
}  
void main ()  
{  
    class arc a;  
    clrscr();  
    a.map();  
    a.graph();  
    a.get();  
    a.cal();  
    a.plot();  
    a.plot1();  
    getch();  
}

  

Output: