Asymptotic Notations or Growth of Functions

Asymptotic Notations are used to describe the execution time of an algorithm. The notations show the order of growth of functions. Here the time taken by an algorithm is mapped regarding mathematical functions. There are many asymptotic notations like 0, θ, Ω,w each having its importance.

1. Big-oh notation: The function f (n) =O (g (n)) [read as "f of n is big-oh of g of n"] if and only if exist positive constant c and n₀ such that

f (n) ⩽ C x g (n) for all n, n ≥ n0

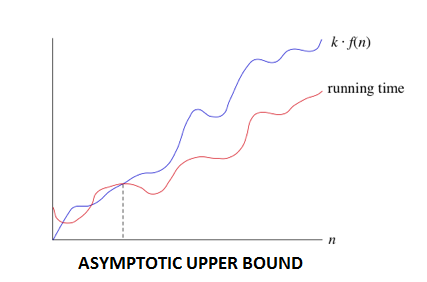
Example1: The function 4n + 3 = O (n) as 4n + 3 ⩽ 5n for all n ≥.

Example2: The function 20n² + 5n + 2 = O (n²) as 20n²+ 5n +2⩽21n² for all n ≥.

2. Omega (Ω) Notation: The function f (n) = Ω (g (n)) [read as "f of n is omega of g of n"] if and only if there exists positive constant c and n₀ such that

f (n) ≥ C* g (n) for all n, n ≥ n0

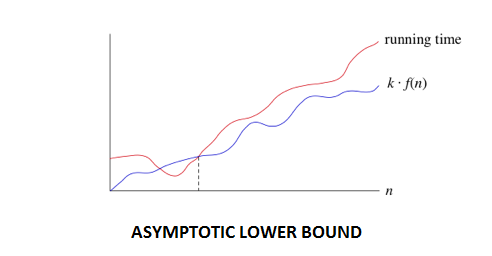
Example1: The function 4n + 3 = Ω (n) as 4n + 3 ≥ 4n for all n ≥1.

Example2: The function 20n²+ 5n +2 = Ω (n) as 20n²+ 5n +2 ≥ 20n² for all n ≥1.

3. Theta (θ): The function f (n) = θ (g (n)) [read as "f is the theta of g of n"] if and only if there exists positive constant k₁, k₂ and k₀ such that

k1* g (n) ≤ f (n)≤k2* g(n)for all n, n≥n0

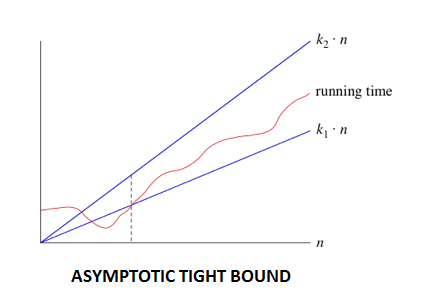
Example1: The function 4n + 3 = θ (n) as 4n + 3 ≥ 4n for all n ≥ 3 and 4n + 3 ≤ 5n for all n ≥ 3.

Example2: The function 20n²+ 5n +2 = θ (n²) as 20n²+ 5n +2 ≤ 21n² for all n ≥1 and 20n²+ 5n +2 ≥ 20n² for all n ≥ 1.