Mathematical Functions

The following are the functions which are widely used in computer science.

1. Floor Functions: The floor function for any real number x is defined as f (x) is the greatest integer 1 less than or equal to x. It is denoted by [x].

Example: Determine the value of

(i)[3. 5]       (ii)[-2.4]       (iii)[3. 143].

Solution:

(i)[3 . 5]  = 3
(ii) [-2 .4] = -3
(iii) [3. 143] = 3

2. Ceiling Functions: The ceiling function for any real number x is defined as h (x) is the smallest integer greater than or equal to x. It is denoted by [x].

Example: Determine the value of

(i)[3. 5]       (ii) [-2.4]       (iii) [3. 143].

Solution:

 
(i)[3. 5] = 4
(ii) [-2 .4] = -2
(iii) [3. 143] = 4.

3. Remainder Functions: The integer remainder is obtained when some a is divided by m. It is denoted by a (MOD m). We can also define it as, a (MOD m) is the unique integer t such that a = Mq + t. Here q is quotient 0 ≤ r < M.

Example: Determine the value of the following:

(i) 35 (MOD 7)       (ii) 20 (MOD 3)       (iii) 4 (MOD 9)

Solution:

(i) 35 (MOD 7) = 0
(ii) 20 (MOD 3) = 2
(iii) 4 (MOD 9) = 4

4. Exponential Functions: Consider two sets A and B. Let A = B = I₊ and also let f: A → B be defined by f (n) = kⁿ. Here n is a +ve integer. The function f is called the base k exponential function.

Note1: k^t= k. k. k.......k (t times).
2: k⁰=1,k^-M=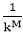
3. For rational number, a/b, the exponential function is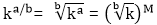

Example: Determine the value of the following:

(i) 10³       (ii) 5^1/2       (iii) 3^-5

Solution:

103= 10. 10. 10 = 1000
51/2=2.23607
3-5=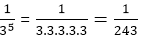

5. Logarithmic Functions: Consider two sets A and B. Let A = B = R (the set of real numbers and also let f_n:A→B be defined for each positive integer n > 1 as f_n (x)=log_n(x) the base n of x.

Note1: k = log_n x and n^k are equivalent.
2. For any base n, log_n 1=0 as n⁰=1.
3. For any base n, log_n n=1 as n¹=n.

Example: Determine the value of the following:

(i) log₂?16       (ii) log₂ 100       (iii) log_2 0.001.

Solution:

(i)log216 = 4 as 24=16.                                          
(ii)log2 100 = 6 as 26= 64 but 27=128 which is greater
(iii)log2 0.001=-9 as 2-9=but 2-10=which is greater.