DAG representation for basic blocks

A DAG for basic block is a directed acyclic graph with the following labels on nodes:

1. The leaves of graph are labeled by unique identifier and that identifier can be variable names or constants.
2. Interior nodes of the graph is labeled by an operator symbol.
3. Nodes are also given a sequence of identifiers for labels to store the computed value.

• DAGs are a type of data structure. It is used to implement transformations on basic blocks.
• DAG provides a good way to determine the common sub-expression.
• It gives a picture representation of how the value computed by the statement is used in subsequent statements.

Algorithm for construction of DAG

Input:It contains a basic block

Output: It contains the following information:

• Each node contains a label. For leaves, the label is an identifier.
• Each node contains a list of attached identifiers to hold the computed values.

1. Case (i) x:= y OP z  
2.    Case (ii) x:= OP y  
3.    Case (iii) x:= y  

Method:

Step 1:

If y operand is undefined then create node(y).

If z operand is undefined then for case(i) create node(z).

Step 2:

For case(i), create node(OP) whose right child is node(z) and left child is node(y).

For case(ii), check whether there is node(OP) with one child node(y).

For case(iii), node n will be node(y).

Output:

For node(x) delete x from the list of identifiers. Append x to attached identifiers list for the node n found in step 2. Finally set node(x) to n.

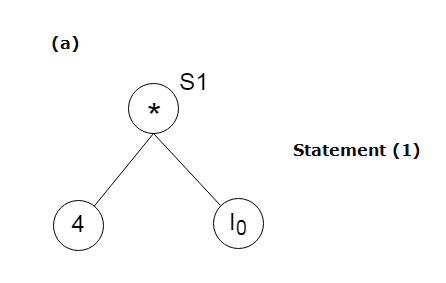
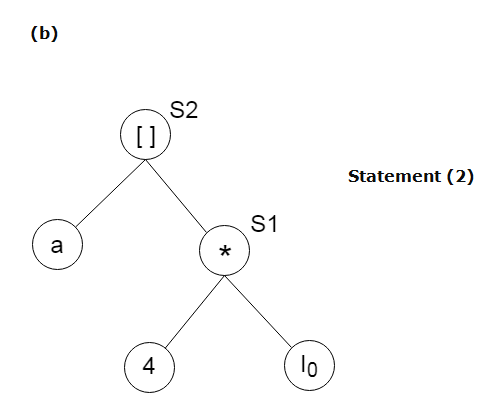
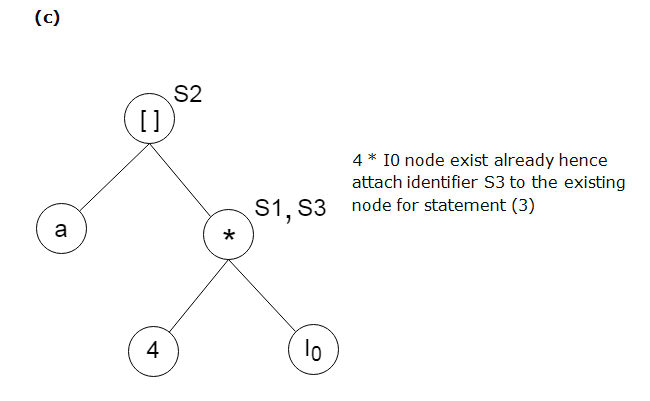
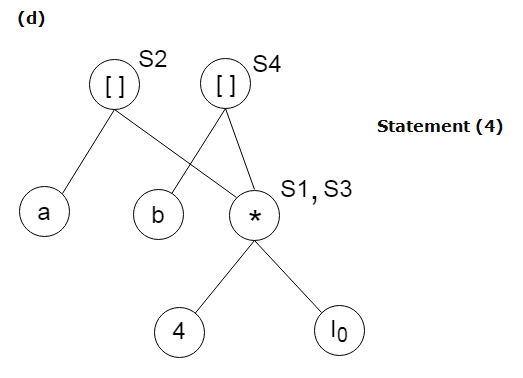
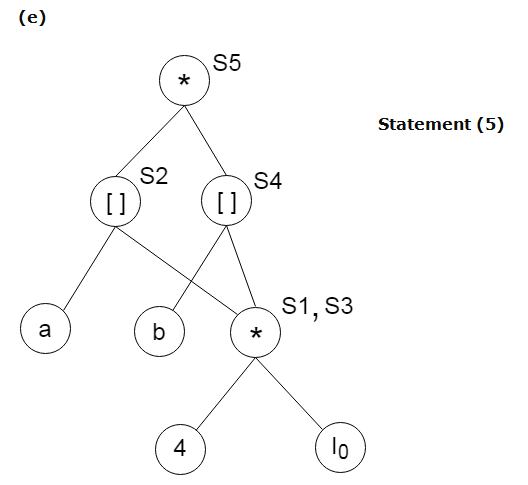
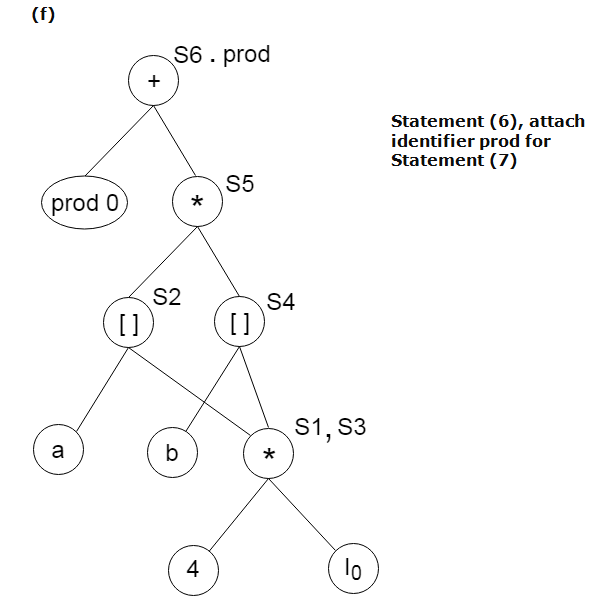
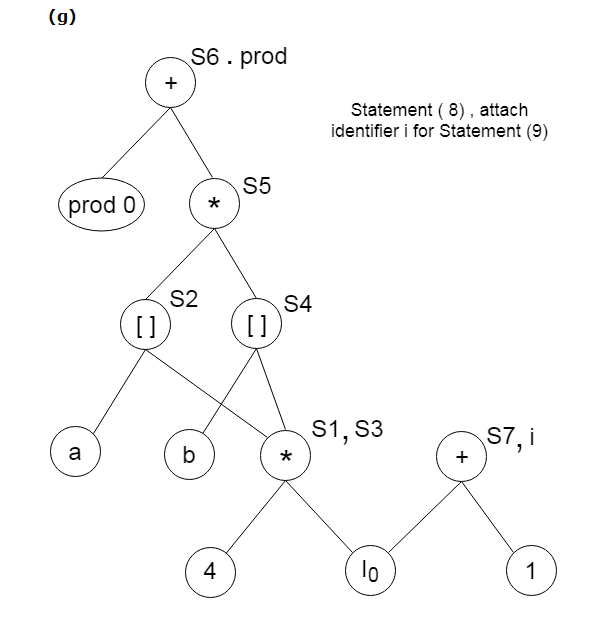
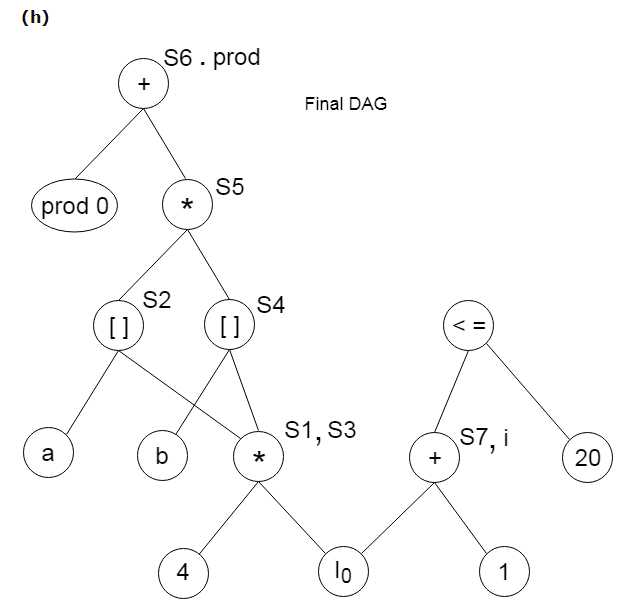
Example:

Consider the following three address statement:

1. S1:= 4 * i  
2. S2:= a[S1]  
3. S3:= 4 * i  
4. S4:= b[S3]    
5. S5:= s2 * S4  
6. S6:= prod + S5  
7. Prod:= s6  
8. S7:= i+1  
9. i := S7  
10. if i<= 20 goto (1)   

Stages in DAG Construction: