Loop Optimization

Loop optimization is most valuable machine-independent optimization because program's inner loop takes bulk to time of a programmer.

If we decrease the number of instructions in an inner loop then the running time of a program may be improved even if we increase the amount of code outside that loop.

For loop optimization the following three techniques are important:

1. Code motion
2. Induction-variable elimination
3. Strength reduction

1.Code Motion:

Code motion is used to decrease the amount of code in loop. This transformation takes a statement or expression which can be moved outside the loop body without affecting the semantics of the program.

For example

In the while statement, the limit-2 equation is a loop invariant equation.

1. while (i<=limit-2)     /*statement does not change limit*/  
2. After code motion the result is as follows:  
3.           a= limit-2;  
4.           while(i<=a)    /*statement does not change limit or a*/  

2.Induction-Variable Elimination

Induction variable elimination is used to replace variable from inner loop.

It can reduce the number of additions in a loop. It improves both code space and run time performance.

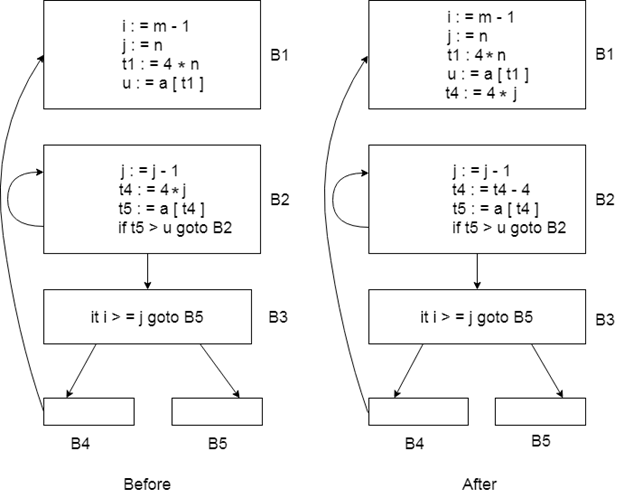
In this figure, we can replace the assignment t4:=4*j by t4:=t4-4. The only problem which will be arose that t4 does not have a value when we enter block B2 for the first time. So we place a relation t4=4*j on entry to the block B2.

3.Reduction in Strength

• Strength reduction is used to replace the expensive operation by the cheaper once on the target machine.
• Addition of a constant is cheaper than a multiplication. So we can replace multiplication with an addition within the loop.
• Multiplication is cheaper than exponentiation. So we can replace exponentiation with multiplication within the loop.

Example:

1. while (i<10)  
2.         {  
3. j= 3 * i+1;  
4. a[j]=a[j]-2;  
5. i=i+2;  
6.         }  

After strength reduction the code will be:

1. s= 3*i+1;  
2.       while (i<10)  
3.        {  
4.             j=s;  
5.             a[j]= a[j]-2;  
6.             i=i+2;  
7.             s=s+6;  
8.        }  

In the above code, it is cheaper to compute s=s+6 than j=3 *i