2D array can be defined as an array of arrays. The 2D array is organized as matrices which can be represented as the collection of rows and columns.
However, 2D arrays are created to implement a relational database look alike data structure. It provides ease of holding bulk of data at once which can be passed to any number of functions wherever required.
How to declare 2D Array
The syntax of declaring two dimensional array is very much similar to that of a one dimensional array, given as follows.
int arr[max_rows][max_columns];
however, It produces the data structure which looks like following.6M
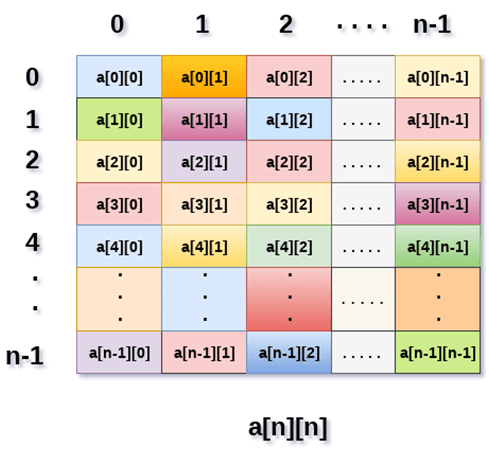
Above image shows the two dimensional array, the elements are organized in the form of rows and columns. First element of the first row is represented by a[0][0] where the number shown in the first index is the number of that row while the number shown in the second index is the number of the column.
How do we access data in a 2D array
Due to the fact that the elements of 2D arrays can be random accessed. Similar to one dimensional arrays, we can access the individual cells in a 2D array by using the indices of the cells. There are two indices attached to a particular cell, one is its row number while the other is its column number.
However, we can store the value stored in any particular cell of a 2D array to some variable x by using the following syntax.
int x = a[i][j];
where i and j is the row and column number of the cell respectively.
We can assign each cell of a 2D array to 0 by using the following code:
for ( int i=0; i<n ;i++){
for (int j=0; j<n; j++)
{
a[i][j] = 0;
}
}
Initializing 2D Arrays
We know that, when we declare and initialize one dimensional array in C programming simultaneously, we don't need to specify the size of the array. However this will not work with 2D arrays. We will have to define at least the second dimension of the array.
The syntax to declare and initialize the 2D array is given as follows.
int arr[2][2] = {0,1,2,3};The number of elements that can be present in a 2D array will always be equal to (number of rows * number of columns).
Example : Storing User's data into a 2D array and printing it.
C Example :
#include <stdio.h>void main ()
{
int arr[3][3],i,j;
for (i=0;i<3;i++)
{
for (j=0;j<3;j++)
{
printf("Enter a[%d][%d]: ",i,j);
scanf("%d",&arr[i][j]);
}
}
printf("\n printing the elements ....\n");
for(i=0;i<3;i++)
{
printf("\n");
for (j=0;j<3;j++)
{
printf("%d\t",arr[i][j]);
}
}
}
Mapping 2D array to 1D array
When it comes to map a 2 dimensional array, most of us might think that why this mapping is required. However, 2 D arrays exists from the user point of view. 2D arrays are created to implement a relational database table lookalike data structure, in computer memory, the storage technique for 2D array is similar to that of an one dimensional array.
The size of a two dimensional array is equal to the multiplication of number of rows and the number of columns present in the array. We do need to map two dimensional array to the one dimensional array in order to store them in the memory.
A 3 X 3 two dimensional array is shown in the following image. However, this array needs to be mapped to a one dimensional array in order to store it into the memory.
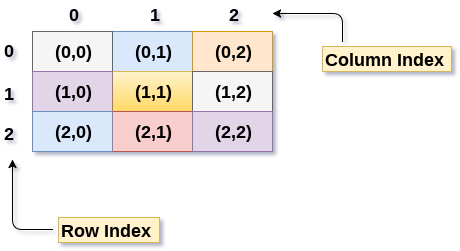
There are two main techniques of storing 2D array elements into memory
1. Row Major ordering
In row major ordering, all the rows of the 2D array are stored into the memory contiguously. Considering the array shown in the above image, its memory allocation according to row major order is shown as follows.
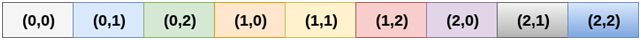
first, the 1st row of the array is stored into the memory completely, then the 2nd row of the array is stored into the memory completely and so on till the last row.
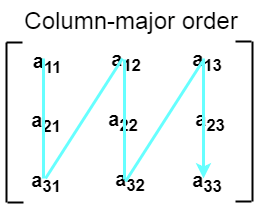
2. Column Major ordering
According to the column major ordering, all the columns of the 2D array are stored into the memory contiguously. The memory allocation of the array which is shown in in the above image is given as follows.
first, the 1st column of the array is stored into the memory completely, then the 2nd row of the array is stored into the memory completely and so on till the last column of the array.
Calculating the Address of the random element of a 2D array
Due to the fact that, there are two different techniques of storing the two dimensional array into the memory, there are two different formulas to calculate the address of a random element of the 2D array.
By Row Major Order
If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as,
Address of A[I][J] = B + W * ((I – LR) * N + (J – LC))
I = Row Subset of an element whose address to be found,
J = Column Subset of an element whose address to be found,
B = Base address,
W = Storage size of one element store in an array(in byte),
LR = Lower Limit of row/start row index of the matrix(If not given assume it as zero),
LC = Lower Limit of column/start column index of the matrix(If not given assume it as zero),
N = Number of column given in the matrix.
where, B. A. is the base address or the address of the first element of the array a[0][0] .
Example: Given an array, arr[1………10][1………15] with base value 100 and the size of each element is 1 Byte in memory. Find the address of arr[8][6] with the help of row-major order.
Solution:
Ques. Given an array [1…5,1…7] of integers. Calculate address of element T[4,6], where BA=900.Given:
Base address B = 100
Storage size of one element store in any array W = 1 Bytes
Row Subset of an element whose address to be found I = 8
Column Subset of an element whose address to be found J = 6
Lower Limit of row/start row index of matrix LR = 1
Lower Limit of column/start column index of matrix = 1
Number of column given in the matrix N = Upper Bound – Lower Bound + 1
= 15 – 1 + 1
= 15Formula:
Address of A[I][J] = B + W * ((I – LR) * N + (J – LC))Solution:
Address of A[8][6] = 100 + 1 * ((8 – 1) * 15 + (6 – 1))
= 100 + 1 * ((7) * 15 + (5))
= 100 + 1 * (110)
Address of A[I][J] = 210
Solution:- I = 4 , J = 6 ,M= 5 , N= 7
Location (T [4,6]) = BA + (7 x (4-1)) + (6-1)
= 900+ (7 x 3) +5
= 900+ 21 + 5
= 926
By Column major order
If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as,
Address of A[I][J] = B + W * ((J – LC) * M + (I – LR))
I = Row Subset of an element whose address to be found,
J = Column Subset of an element whose address to be found,
B = Base address,
W = Storage size of one element store in any array(in byte),
LR = Lower Limit of row/start row index of matrix(If not given assume it as zero),
LC = Lower Limit of column/start column index of matrix(If not given assume it as zero),
M = Number of rows given in the matrix.
Example: Given an array arr[1………10][1………15] with a base value of 100 and the size of each element is 1 Byte in memory find the address of arr[8][6] with the help of column-major order.
Solution:
Ques. Given an array [1…6,1…8] of integers. Calculate address element T[5,7], where BA=300.Given:
Base address B = 100
Storage size of one element store in any array W = 1 Bytes
Row Subset of an element whose address to be found I = 8
Column Subset of an element whose address to be found J = 6
Lower Limit of row/start row index of matrix LR = 1
Lower Limit of column/start column index of matrix = 1
Number of column given in the matrix M = Upper Bound – Lower Bound + 1
= 10 – 1 + 1
= 10Formula: used
Address of A[I][J] = B + W * ((J – LC) * M + (I – LR))
Address of A[8][6] = 100 + 1 * ((6 – 1) * 10 + (8 – 1))
= 100 + 1 * ((5) * 10 + (7))
= 100 + 1 * (57)
Address of A[I][J] = 157
Solution:- I = 5 , J = 7, M= 6 , N= 8
Location (T [4,6]) = BA + (6 x (7-1)) + (5-1)
= 300+ (6 x 6) +4
= 300+ 36+4
= 340
Ques 20 Consider the linear arrays AAA [5:50], BBB [-5:10] and CCC[1:8].
1. Find the number of elements in each array.
2. Suppose base (AAA) = 300 and w = 4 words per memory cell for AAA. find the address of AAA [15], AAA [35] and AAA [55].
AKTU 2015-16, Marks 10
Answer:




No comments:
Post a Comment