Graph Representations

A graph is a data structure that consist a sets of vertices (called nodes) and edges. There are two ways to store Graphs into the computer's memory:

• Sequential representation (or, Adjacency matrix representation)
• Linked list representation (or, Adjacency list representation)

In sequential representation, an adjacency matrix is used to store the graph. Whereas in linked list representation, there is a use of an adjacency list to store the graph.

In this tutorial, we will discuss each one of them in detail.

Now, let's start discussing the ways of representing a graph in the data structure.

Sequential representation

In sequential representation, there is a use of an adjacency matrix to represent the mapping between vertices and edges of the graph. We can use an adjacency matrix to represent the undirected graph, directed graph, weighted directed graph, and weighted undirected graph.

If adj[i][j] = w, it means that there is an edge exists from vertex i to vertex j with weight w.

An entry A_ij in the adjacency matrix representation of an undirected graph G will be 1 if an edge exists between V_i and V_j. If an Undirected Graph G consists of n vertices, then the adjacency matrix for that graph is n x n, and the matrix A = [aij] can be defined as -

a_ij = 1 {if there is a path exists from V_i to V_j}

a_ij = 0 {Otherwise}

It means that, in an adjacency matrix, 0 represents that there is no association exists between the nodes, whereas 1 represents the existence of a path between two edges.

If there is no self-loop present in the graph, it means that the diagonal entries of the adjacency matrix will be 0.

Now, let's see the adjacency matrix representation of an undirected graph.

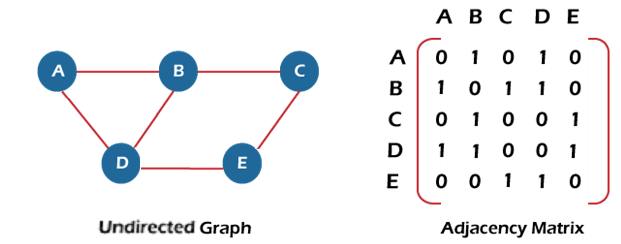
In the above figure, an image shows the mapping among the vertices (A, B, C, D, E), and this mapping is represented by using the adjacency matrix.

There exist different adjacency matrices for the directed and undirected graph. In a directed graph, an entry A_ij will be 1 only when there is an edge directed from V_i to V_j.

Adjacency matrix for a directed graph

In a directed graph, edges represent a specific path from one vertex to another vertex. Suppose a path exists from vertex A to another vertex B; it means that node A is the initial node, while node B is the terminal node.

Consider the below-directed graph and try to construct the adjacency matrix of it.

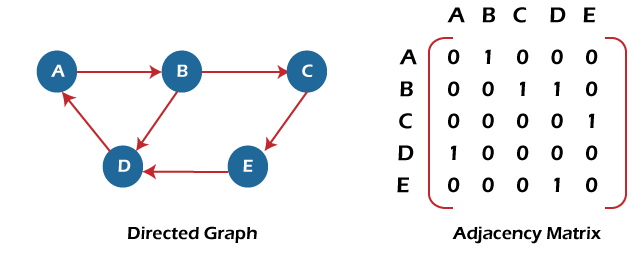
In the above graph, we can see there is no self-loop, so the diagonal entries of the adjacent matrix are 0.

Adjacency matrix for a weighted directed graph

It is similar to an adjacency matrix representation of a directed graph except that instead of using the '1' for the existence of a path, here we have to use the weight associated with the edge. The weights on the graph edges will be represented as the entries of the adjacency matrix. We can understand it with the help of an example. Consider the below graph and its adjacency matrix representation. In the representation, we can see that the weight associated with the edges is represented as the entries in the adjacency matrix.

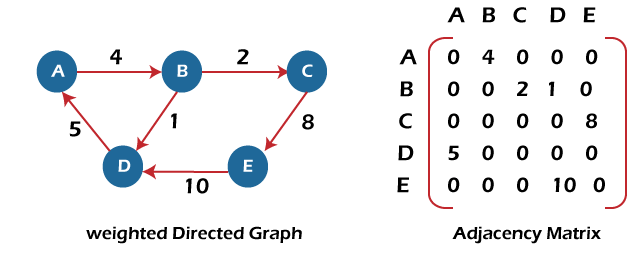
In the above image, we can see that the adjacency matrix representation of the weighted directed graph is different from other representations. It is because, in this representation, the non-zero values are replaced by the actual weight assigned to the edges.

Adjacency matrix is easier to implement and follow. An adjacency matrix can be used when the graph is dense and a number of edges are large.

Though, it is advantageous to use an adjacency matrix, but it consumes more space. Even if the graph is sparse, the matrix still consumes the same space.

Linked list representation

An adjacency list is used in the linked representation to store the Graph in the computer's memory. It is efficient in terms of storage as we only have to store the values for edges.

Let's see the adjacency list representation of an undirected graph.

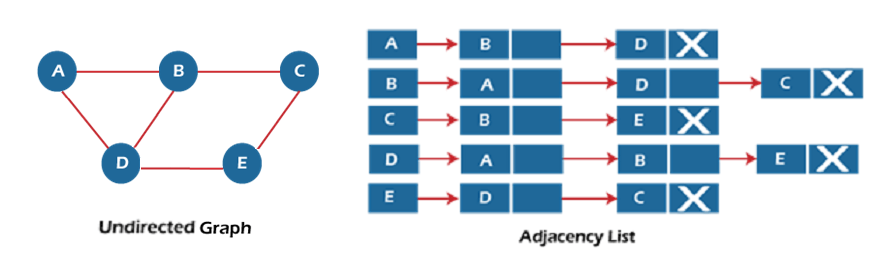
In the above figure, we can see that there is a linked list or adjacency list for every node of the graph. From vertex A, there are paths to vertex B and vertex D. These nodes are linked to nodes A in the given adjacency list.

An adjacency list is maintained for each node present in the graph, which stores the node value and a pointer to the next adjacent node to the respective node. If all the adjacent nodes are traversed, then store the NULL in the pointer field of the last node of the list.

The sum of the lengths of adjacency lists is equal to twice the number of edges present in an undirected graph.

Now, consider the directed graph, and let's see the adjacency list representation of that graph.

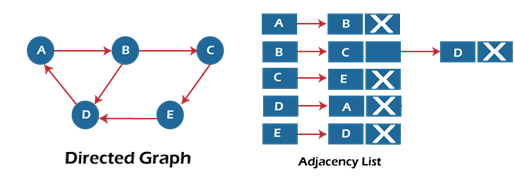
For a directed graph, the sum of the lengths of adjacency lists is equal to the number of edges present in the graph.

Now, consider the weighted directed graph, and let's see the adjacency list representation of that graph.

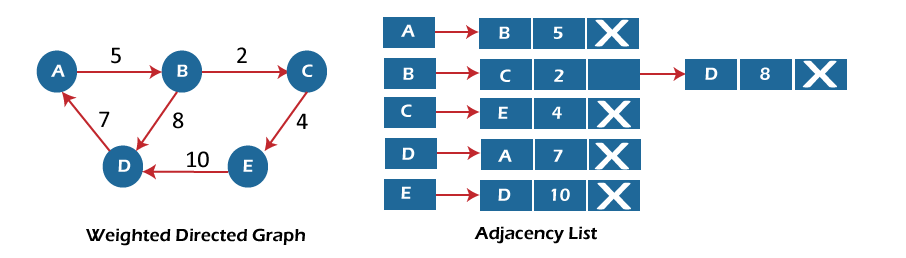
In the case of a weighted directed graph, each node contains an extra field that is called the weight of the node.

In an adjacency list, it is easy to add a vertex. Because of using the linked list, it also saves space.

Implementation of adjacency matrix representation of Graph

Now, let's see the implementation of adjacency matrix representation of graph in C.

In this program, there is an adjacency matrix representation of an undirected graph. It means that if there is an edge exists from vertex A to vertex B, there will also an edge exists from vertex B to vertex A.

Here, there are four vertices and five edges in the graph that are non-directed.

// C program for the above approach

#include <stdio.h>

  

// N vertices and M Edges

int N, M;

  

// Function to create Adjacency Matrix

void createAdjMatrix(int Adj[][N + 1],

                     int arr[][2])

{

  

    // Initialise all value to this

    // Adjacency list to zero

    for (int i = 0; i < N + 1; i++) {

  

        for (int j = 0; j < N + 1; j++) {

            Adj[i][j] = 0;

        }

    }

  

    // Traverse the array of Edges

    for (int i = 0; i < M; i++) {

  

        // Find X and Y of Edges

        int x = arr[i][0];

        int y = arr[i][1];

  

        // Update value to 1

        Adj[x][y] = 1;

        Adj[y][x] = 1;

    }

}

  

// Function to print the created

// Adjacency Matrix

void printAdjMatrix(int Adj[][N + 1])

{

  

    // Traverse the Adj[][]

    for (int i = 1; i < N + 1; i++) {

        for (int j = 1; j < N + 1; j++) {

  

            // Print the value at Adj[i][j]

            printf("%d ", Adj[i][j]);

        }

        printf("\n");

    }

}

  

// Driver Code

int main()

{

  

    // Number of vertices

    N = 5;

  

    // Given Edges

    int arr[][2]

        = { { 1, 2 }, { 2, 3 }, 

            { 4, 5 }, { 1, 5 } };

  

    // Number of Edges

    M = sizeof(arr) / sizeof(arr[0]);

  

    // For Adjacency Matrix

    int Adj[N + 1][N + 1];

  

    // Function call to create

    // Adjacency Matrix

    createAdjMatrix(Adj, arr);

  

    // Print Adjacency Matrix

    printAdjMatrix(Adj);

  

    return 0;

}

Output:

After the execution of the above code, the output will be -

0 1 0 0 1 
1 0 1 0 0 
0 1 0 0 0 
0 0 0 0 1 
1 0 0 1 0

Implementation of adjacency list representation of Graph

Now, let's see the implementation of adjacency list representation of graph in C.

In this program, there is an adjacency list representation of an undirected graph. It means that if there is an edge exists from vertex A to vertex B, there will also an edge exists from vertex B to vertex A.

// A C Program to demonstrate adjacency list

// representation of graphs

#include <stdio.h>

#include <stdlib.h>

 

// A structure to represent an adjacency list node

struct AdjListNode {

    int dest;

    struct AdjListNode* next;

};

 

// A structure to represent an adjacency list

struct AdjList {

    struct AdjListNode* head;

};

 

// A structure to represent a graph. A graph

// is an array of adjacency lists.

// Size of array will be V (number of vertices

// in graph)

struct Graph {

    int V;

    struct AdjList* array;

};

 

// A utility function to create a new adjacency list node

struct AdjListNode* newAdjListNode(int dest)

{

    struct AdjListNode* newNode

        = (struct AdjListNode*)malloc(

            sizeof(struct AdjListNode));

    newNode->dest = dest;

    newNode->next = NULL;

    return newNode;

}

 

// A utility function that creates a graph of V vertices

struct Graph* createGraph(int V)

{

    struct Graph* graph

        = (struct Graph*)malloc(sizeof(struct Graph));

    graph->V = V;

 

    // Create an array of adjacency lists.  Size of

    // array will be V

    graph->array = (struct AdjList*)malloc(

        V * sizeof(struct AdjList));

 

    // Initialize each adjacency list as empty by

    // making head as NULL

    int i;

    for (i = 0; i < V; ++i)

        graph->array[i].head = NULL;

 

    return graph;

}

 

// Adds an edge to an undirected graph

void addEdge(struct Graph* graph, int src, int dest)

{

    // Add an edge from src to dest.  A new node is

    // added to the adjacency list of src.  The node

    // is added at the beginning

    struct AdjListNode* check = NULL;

    struct AdjListNode* newNode = newAdjListNode(dest);

 

    if (graph->array[src].head == NULL) {

        newNode->next = graph->array[src].head;

        graph->array[src].head = newNode;

    }

    else {

 

        check = graph->array[src].head;

        while (check->next != NULL) {

            check = check->next;

        }

        // graph->array[src].head = newNode;

        check->next = newNode;

    }

 

    // Since graph is undirected, add an edge from

    // dest to src also

    newNode = newAdjListNode(src);

    if (graph->array[dest].head == NULL) {

        newNode->next = graph->array[dest].head;

        graph->array[dest].head = newNode;

    }

    else {

        check = graph->array[dest].head;

        while (check->next != NULL) {

            check = check->next;

        }

        check->next = newNode;

    }

 

    // newNode = newAdjListNode(src);

    // newNode->next = graph->array[dest].head;

    // graph->array[dest].head = newNode;

}

 

// A utility function to print the adjacency list

// representation of graph

void printGraph(struct Graph* graph)

{

    int v;

    for (v = 0; v < graph->V; ++v) {

        struct AdjListNode* pCrawl = graph->array[v].head;

        printf("\n Adjacency list of vertex %d\n head ", v);

        while (pCrawl) {

            printf("-> %d", pCrawl->dest);

            pCrawl = pCrawl->next;

        }

        printf("\n");

    }

}

 

// Driver program to test above functions

int main()

{

    // create the graph given in above figure

    int V = 5;

    struct Graph* graph = createGraph(V);

    addEdge(graph, 0, 1);

    addEdge(graph, 0, 4);

    addEdge(graph, 1, 2);

    addEdge(graph, 1, 3);

    addEdge(graph, 1, 4);

    addEdge(graph, 2, 3);

    addEdge(graph, 3, 4);

 

    // print the adjacency list representation of the above

    // graph

    printGraph(graph);

 

    return 0;

}

Output:

In the output, we will see the adjacency list representation of all the vertices of the graph. After the execution of the above code, the output will be -

 Adjacency list of vertex 0
 head -> 1-> 4

 Adjacency list of vertex 1
 head -> 0-> 2-> 3-> 4

 Adjacency list of vertex 2
 head -> 1-> 3

 Adjacency list of vertex 3
 head -> 1-> 2-> 4

 Adjacency list of vertex 4
 head -> 0-> 1-> 3