Graph
A graph can be defined as group of vertices and edges that are used to connect these vertices. A graph can be seen as a cyclic tree, where the vertices (Nodes) maintain any complex relationship among them instead of having parent child relationship.
Definition
A graph G can be defined as an ordered set G(V, E) where V(G) represents the set of vertices and E(G) represents the set of edges which are used to connect these vertices.
A Graph G(V, E) with 5 vertices (A, B, C, D, E) and six edges ((A,B), (B,C), (C,E), (E,D), (D,B), (D,A)) is shown in the following figure.
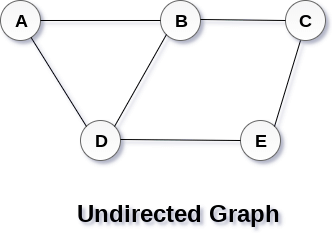
Directed and Undirected Graph
A graph can be directed or undirected. However, in an undirected graph, edges are not associated with the directions with them. An undirected graph is shown in the above figure since its edges are not attached with any of the directions. If an edge exists between vertex A and B then the vertices can be traversed from B to A as well as A to B.
In a directed graph, edges form an ordered pair. Edges represent a specific path from some vertex A to another vertex B. Node A is called initial node while node B is called terminal node.
A directed graph is shown in the following figure.
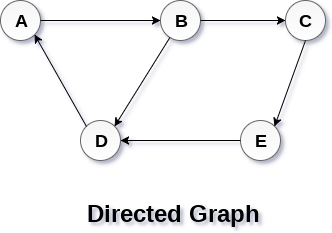
Graph Terminology
Path
A path can be defined as the sequence of nodes that are followed in order to reach some terminal node V from the initial node U.
Closed Path
A path will be called as closed path if the initial node is same as terminal node. A path will be closed path if V0=VN.
Simple Path
If all the nodes of the graph are distinct with an exception V0=VN, then such path P is called as closed simple path.
Cycle
A cycle can be defined as the path which has no repeated edges or vertices except the first and last vertices.
Connected Graph
A connected graph is the one in which some path exists between every two vertices (u, v) in V. There are no isolated nodes in connected graph.
Complete Graph
A complete graph is the one in which every node is connected with all other nodes. A complete graph contain n(n-1)/2 edges where n is the number of nodes in the graph.
Weighted Graph
In a weighted graph, each edge is assigned with some data such as length or weight. The weight of an edge e can be given as w(e) which must be a positive (+) value indicating the cost of traversing the edge.
Digraph
A digraph is a directed graph in which each edge of the graph is associated with some direction and the traversing can be done only in the specified direction.
Loop
An edge that is associated with the similar end points can be called as Loop.
Adjacent Nodes
If two nodes u and v are connected via an edge e, then the nodes u and v are called as neighbours or adjacent nodes.
Degree of the Node
A degree of a node is the number of edges that are connected with that node. A node with degree 0 is called as isolated node.
So depending upon the position of these nodes and vertices, there are different types of graphs, such as:
- Null Graph
- Trivial Graph
- Non-directed Graph
- Directed Graph
- Connected Graph
- Disconnected Graph
- Regular Graph
- Complete Graph
- Cycle Graph
- Cyclic Graph
- Acyclic Graph
- Finite Graph
- Infinite Graph
- Bipartite Graph
- Planar Graph
- Simple Graph
- Multi Graph
- Pseudo Graph
- Euler Graph
- Hamiltonian Graph
Null Graph
The Null Graph is also known as the order zero graph. The term "null graph" refers to a graph with an empty edge set. In other words, a null graph has no edges, and the null graph is present with only isolated vertices in the graph.
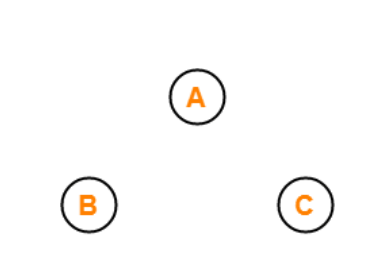
The image displayed above is a null or zero graphs because it has zero edges between the three vertices of the graph.
Trivial Graph
A graph is called a trivial graph if it has only one vertex present in it. The trivial graph is the smallest possible graph that can be created with the least number of vertices that is one vertex only.

The above is an example of a trivial graph having only a single vertex in the whole graph named vertices A.
Non-Directed Graph
A graph is called a non-directed graph if all the edges present between any graph nodes are non-directed. By non-directed edges, we mean the edges of the graph that cannot be determined from the node it is starting and at which node it is ending. All the edges for a graph need to be non-directed to call it a non-directed graph. All the edges of a non-directed graph don't have any direction.
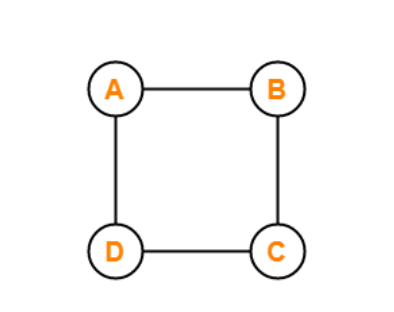
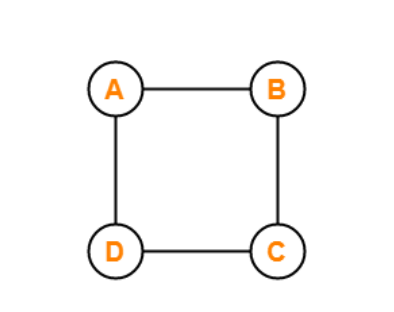
The graph that is displayed above is an example of a disconnected graph. This graph is called a disconnected graph because there are four vertices named vertex A, vertex B, vertex C, and vertex D. There are also exactly four edges between these vertices of the graph. And all the vertices that are present between the different nodes of the graph are not directed, which means the edges don't have any specific direction.
For example, the edge between vertex A and vertex B doesn't have any direction, so we cannot determine whether the edge between vertex A and vertex B starts from vertex A or vertex B. Similarly, we can't determine the ending vertex of this edge between these nodes.
Directed Graph
Another name for the directed graphs is digraphs. A graph is called a directed graph or digraph if all the edges present between any vertices or nodes of the graph are directed or have a defined direction. By directed edges, we mean the edges of the graph that have a direction to determine from which node it is starting and at which node it is ending.
All the edges for a graph need to be directed to call it a directed graph or digraph. All the edges of a directed graph or digraph have a direction that will start from one vertex and end at another.
The graph that is displayed above is an example of a connected graph. This graph is called a connected graph because there are four vertices in the graph named vertex A, vertex B, vertex C, and vertex D. There are also exactly four edges between these vertices of the graph and all the vertices that are present between the different nodes of the graph are directed (or pointing to some of the vertices) which means the edges have a specific direction assigned to them.
For example, consider the edge that is present between vertex D and vertex A. This edge shows that an arrowhead is pointing towards vertex A, which means this edge starts from vertex D and ends at vertex A.
Connected Graph
For a graph to be labelled as a connected graph, there must be at least a single path between every pair of the graph's vertices. In other words, we can say that if we start from one vertex, we should be able to move to any of the vertices that are present in that particular graph, which means there exists at least one path between all the vertices of the graph.
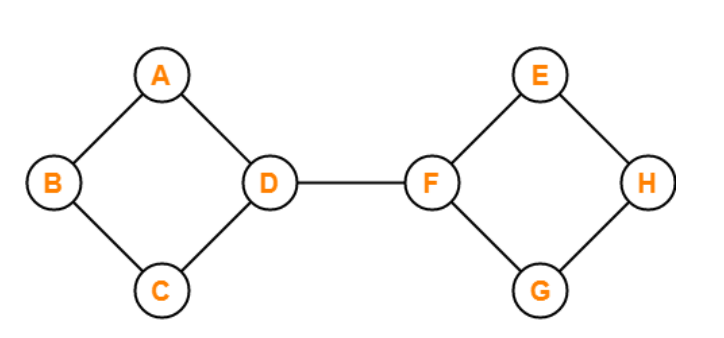
The graph shown above is an example of a connected graph because we start from any one of the vertices of the graph and start moving towards any other remaining vertices of the graph. There will exist at least one path for traversing the graph.
For example, if we begin from vertex B and traverse to vertex H, there are various paths for traversing. One of the paths is
Vertice B -> vertice C -> vertice D -> vertice F -> vertice E -> vertice H.
Similarly, there are other paths for traversing the graph from vertex B to vertex H. there is at least one path between all the graph nodes. In other words, we can say that all the vertices or nodes of the graph are connected to each other via edge or number of edges.
Disconnected Graph
A graph is said to be a disconnected graph where there does not exist any path between at least one pair of vertices. In other words, we can say that if we start from any one of the vertices of the graph and try to move to the remaining present vertices of the graph and there exists not even a single path to move to that vertex, then it is the case of the disconnected graph. If any one of such a pair of vertices doesn't have a path between them, it is called a disconnected graph.
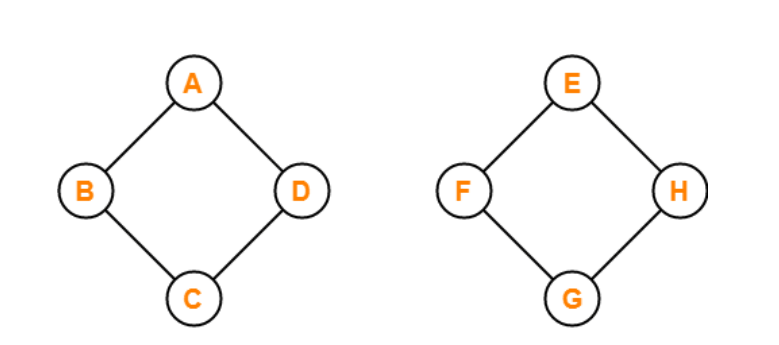
The graph shown above is a disconnected graph. The above graph is called a disconnected graph because at least one pair of vertices doesn't have a path to traverse starting from either node.
For example, a single path between both vertices doesn't exist if we want to traverse from vertex A to vertex G. In other words, we can say that all the vertices or nodes of the graph are not connected to each other via edge or number of edges so that they can be traversed.
Regular Graph
For a graph to be called a regular, it should satisfy one primary condition: all graph vertices should have the same degree. By the degree of vertices, we mean the number of nodes associated with a particular vertex. If all the graph nodes have the same degree value, then the graph is called a regular graph. If all the vertices of a graph have the degree value of 6, then the graph is called a 6-regular graph. If all the vertices in a graph are of degree 'k', then it is called a "k-regular graph".
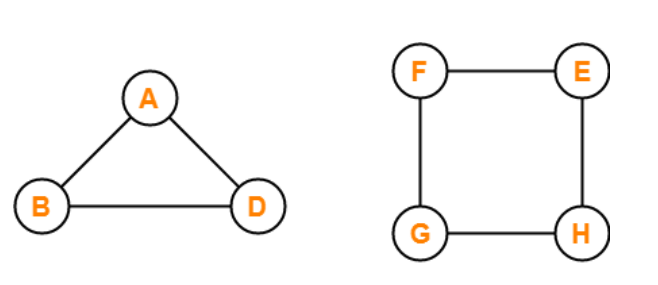
The graphs that are displayed above are regular graphs. In graph 1, there are three vertices named vertex A, vertex B, and vertex C, All the vertices in graph 1, have the degree of each node as 2. The degree of each vertex is calculated by counting the number of edges connected to that particular vertex.
For vertex A in graph 1, there are two edges associated with vertex A, one from vertex B and another from vertex D. Thus, the degree of vertex A of graph one is 2. Similarly, for other vertices of the graph, there are only two edges associated with each vertex, vertex B and vertex D. Therefore, vertex B and vertex D are 2. As the degree of all the three nodes of the graph is the same, that is 2. Therefore, this graph is called a 2-regular graph.
Similarly, for the second graph shown above, there are four vertices named vertex E, vertex F, vertex G, and vertex F. The degree of all the four vertices of this graph is 2. Each vertex of the graph is 2 because only two edges are associated with all of the graph's vertices. As all the nodes of this graph have the same degree of 2, this graph is called a regular graph.
Complete Graph
A graph is said to be a complete graph if, for all the vertices of the graph, there exists an edge between every pair of the vertices. In other words, we can say that all the vertices are connected to the rest of all the vertices of the graph. A complete graph of 'n' vertices contains exactly nC2 edges, and a complete graph of 'n' vertices is represented as Kn.
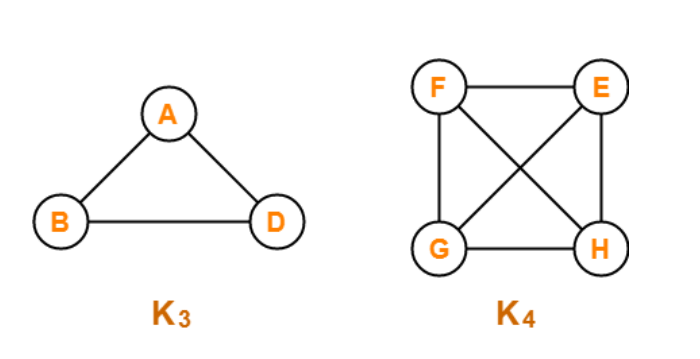
There are two graphs name K3 and K4 shown in the above image, and both graphs are complete graphs. Graph K3 has three vertices, and each vertex has at least one edge with the rest of the vertices. Similarly, for graph K4, there are four nodes named vertex E, vertex F, vertex G, and vertex H. For example, the vertex F has three edges connected to it to connect it to the respective three remaining vertices of the graph. Likewise, for the other three reaming vertices, there are three edges associated with each one of them. As all the vertices of this graph have a separate edge for other vertices, it is called a complete graph.
Cycle Graph
If a graph with many vertices greater than three and edges form a cycle, then the graph is called a cycle graph. In a graph of cycle type, the degree of all the vertices of the cycle graph will be 2.
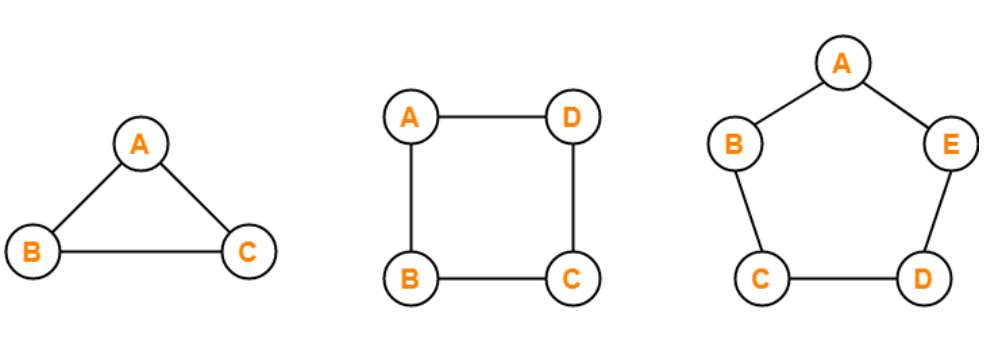
There are three graphs shown in the above image, and all of them are examples of the cyclic graph because the number of nodes for all of these graphs is greater than two and the degree of all the vertices of all these graphs is exactly 2.
Cyclic Graph
For a graph to be called a cyclic graph, it should consist of at least one cycle. If a graph has a minimum of one cycle present, it is called a cyclic graph.
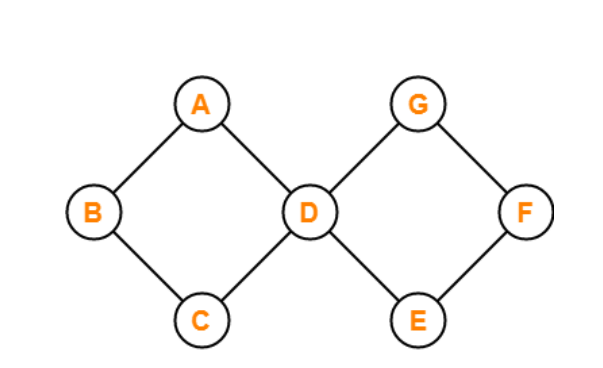
The graph shown in the image has two cycles present, satisfying the required condition for a graph to be cyclic, thus making it a cyclic graph.
Acyclic Graph
A graph is called an acyclic graph if zero cycles are present, and an acyclic graph is the complete opposite of a cyclic graph.
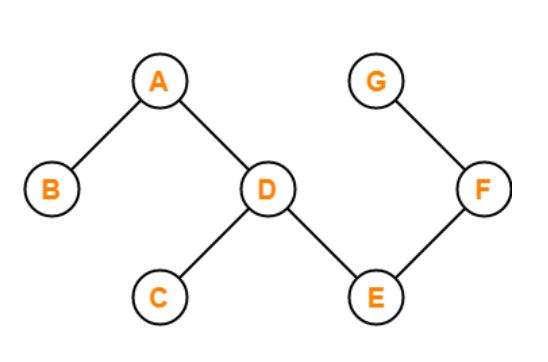
The graph shown in the above image is acyclic because it has zero cycles present in it. That means if we begin traversing the graph from vertex B, then a single path doesn't exist that will traverse all the vertices and end at the same vertex that is vertex B.
Finite Graph
If the number of vertices and the number of edges that are present in a graph are finite in number, then that graph is called a finite graph.
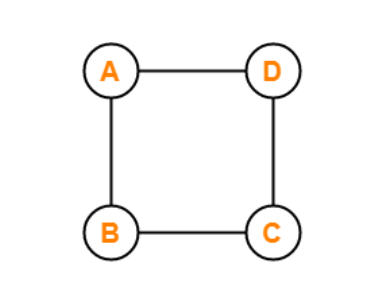
The graph shown in the above image is the finite graph. There are four vertices named vertex A, vertex B, vertex C, and vertex D, and the number of edges present in this graph is also four, as both the number of nodes and vertices of this graph is finite in number it is called a finite graph.
Infinite Graph
If the number of vertices in the graph and the number of edges in the graph are infinite in number, that means the vertices and the edges of the graph cannot be counted, then that graph is called an infinite graph.
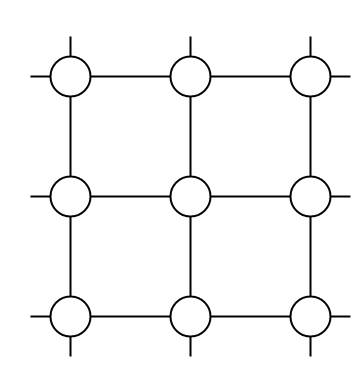
As we can see in the above image, the number of vertices in the graph and the number of edges in the graph are infinite, so this graph is called an infinite graph.
Bipartite Graph
For a graph to be a Bipartite graph, it needs to satisfy some of the basic preconditions. These conditions are:
- All the vertices of the graph should be divided into two distinct sets of vertices X and Y.
- All the vertices present in the set X should only be connected to the vertices present in the set Y with some edges. That means the vertices present in a set should not be connected to the vertex that is present in the same set.
- Both the sets that are created should be distinct that means both should not have the same vertices in them.
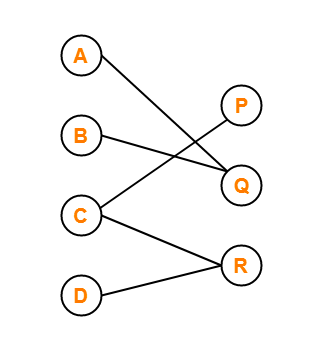
The graph shown in the above image is divided into two vertices named set X and set Y. The contents of these sets are,
Set Y = {vertex P, vertex Q, vertex R}
The vertex A of the set X is associated with the vertex Q of the set Y. And the vertex B is also connected to the vertex Q. The vertex C of the set X is connected to the two vertices of the set Y named vertex P and vertex R. The vertex D of the set X is associated with the vertex Q of the set R.
Similarly, all the vertices present in the set Y are only connected to the vertices from the set X. And both set X and set Y have non-repeating or distinct elements present in them. The graph shown in the above image satisfies all the conditions for the Bipartite graph, and thus it is a Bipartite graph.
Planar Graph
A graph is called a planar graph if that graph can be drawn in a single plane with any two of the edges intersecting each other.
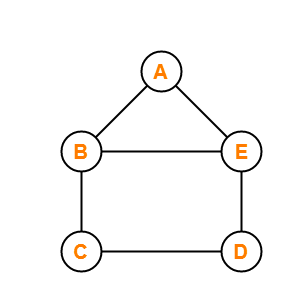
The graph shown in the above image can be drawn in a single plane with any two edges intersecting. Thus it is a planar graph.
Simple Graph
A graph is said to be a simple graph if the graph doesn't consist of no self-loops and no parallel edges in the graph.
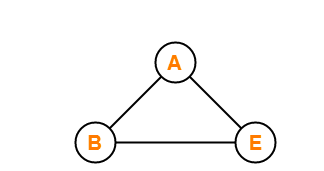
We have three vertices and three edges for the graph that is shown in the above image. This graph has no self-loops and no parallel edges; therefore, it is called a simple graph.
Multi Graph
A graph is said to be a multigraph if the graph doesn't consist of any self-loops, but parallel edges are present in the graph. If there is more than one edge present between two vertices, then that pair of vertices is said to be having parallel edges.
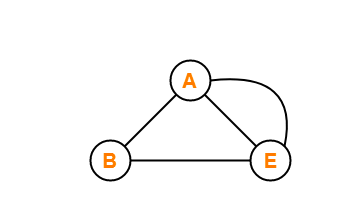
We have three vertices and three edges for the graph that is shown in the above image. There are no self-loops, but two edges connect these two vertices between vertex A and vertex E of the graph. In other words, we can say that if two vertices of a graph are connected with more than one edge in a graph, then it is said to be having parallel edges, thus making it a multigraph.
Pseudo Graph
If a graph consists of no parallel edges, but self-loops are present in a graph, it is called a pseudo graph. The meaning of a self-loop is that there is an edge present in the graph that starts from one of the graph's vertices, and if that edge ends on the same vertex, then it is called a pseudo graph.
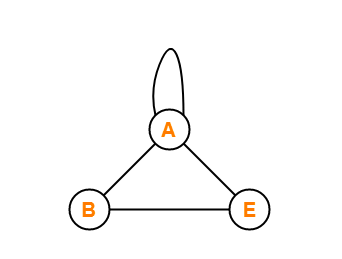
The graph shown in the above image has vertex A, vertex B and vertex E. There are four edges in this graph, and there are three edges associated with vertex A, and among these three edges, one of the edges is a self-loop. And among these four edges present in there is no parallel edge in it. Since the graph shown above has a self-loop and no parallel edge present in it, thus it is a pseudo graph.
Euler Graph
If all the vertices present in a graph have an even degree, then the graph is known as an Euler graph. By degree of a vertex, we mean the number of edges that are associated with a vertex. So for a graph to be an Euler graph, it is required that all the vertices in the graph should be associated with an even number of edges.
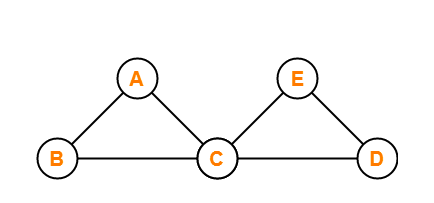
In the graph shown in the above image, we have five vertices named vertex A, vertex B, vertex C, vertex D and vertex E. All the vertices except vertex C have a degree of 2, which means they are associated with two edges each of the vertex. At the same time, vertex C is associated with four edges, thus making it degree 4. The degree of vertex C and other vertices is 4 and 2, respectively, which are even. Therefore, the graph displayed above is an Euler graph.
Hamilton Graph
Suppose a closed walk in the connected graph that visits every vertex of the graph exactly once (except starting vertex) without repeating the edges. Such a graph is called a Hamiltonian graph, and such a walk is called a Hamiltonian path. The Hamiltonian circuit is also known as Hamiltonian Cycle.
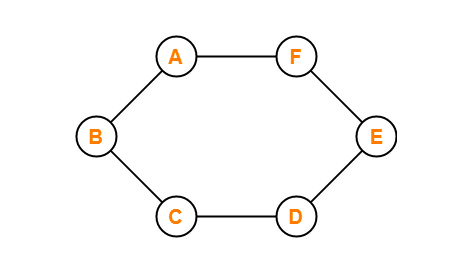
In other words, A Hamiltonian path that starts and ends at the same vertex is called a Hamiltonian circuit. Every graph that contains a Hamiltonian circuit also contains a Hamiltonian path, but vice versa is not true. There may exist more than one Hamiltonian path and Hamiltonian circuit in a graph.
The graph shown in the above image consists of a closed path ABCDEFA which starts from vertex A and traverses all other vertices or nodes without traversing any of the nodes twice other than vertex A in the path of traversal. Therefore, the graph shown in the above image is a Hamilton graph.





No comments:
Post a Comment