Radix Sort Algorithm

Radix sort is the linear sorting algorithm that is used for integers. In Radix sort, there is digit by digit sorting is performed that is started from the least significant digit to the most significant digit.

The process of radix sort works similar to the sorting of students names, according to the alphabetical order. In this case, there are 26 radix formed due to the 26 alphabets in English. In the first pass, the names of students are grouped according to the ascending order of the first letter of their names. After that, in the second pass, their names are grouped according to the ascending order of the second letter of their name. And the process continues until we find the sorted list.

Now, let's see the algorithm of Radix sort.

Algorithm

radixSort(arr)  
max = largest element in the given array  
d = number of digits in the largest element (or, max)  
Now, create d buckets of size 0 - 9  
for i -> 0 to d  
sort the array elements using counting sort (or any stable sort) according to the digits at  
the ith place

Working of Radix sort Algorithm

Now, let's see the working of Radix sort Algorithm.

The steps used in the sorting of radix sort are listed as follows -

• First, we have to find the largest element (suppose max) from the given array. Suppose 'x' be the number of digits in max. The 'x' is calculated because we need to go through the significant places of all elements.
• After that, go through one by one each significant place. Here, we have to use any stable sorting algorithm to sort the digits of each significant place.

Now let's see the working of radix sort in detail by using an example. To understand it more clearly, let's take an unsorted array and try to sort it using radix sort. It will make the explanation clearer and easier.

In the given array, the largest element is 736 that have 3 digits in it. So, the loop will run up to three times (i.e., to the hundreds place). That means three passes are required to sort the array.

Now, first sort the elements on the basis of unit place digits (i.e., x = 0). Here, we are using the counting sort algorithm to sort the elements.

Pass 1:

In the first pass, the list is sorted on the basis of the digits at 0's place.

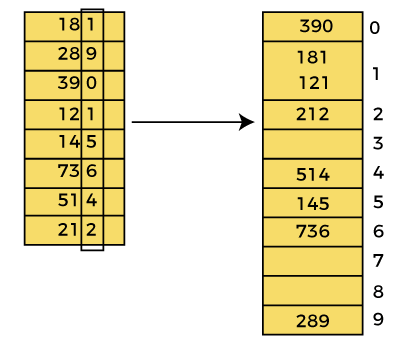
After the first pass, the array elements are -

Pass 2:

In this pass, the list is sorted on the basis of the next significant digits (i.e., digits at 10^th place).

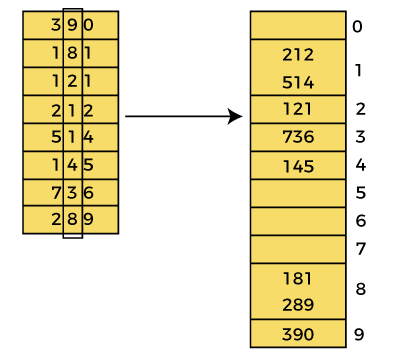
After the second pass, the array elements are -

Pass 3:

In this pass, the list is sorted on the basis of the next significant digits (i.e., digits at 100^th place).

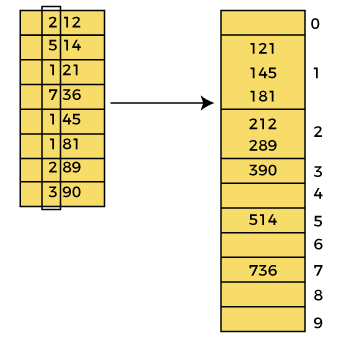
After the third pass, the array elements are -

Now, the array is sorted in ascending order.

Radix sort complexity

Now, let's see the time complexity of Radix sort in best case, average case, and worst case. We will also see the space complexity of Radix sort.

1. Time Complexity

Case	Time Complexity
Best Case	Ω(n+k)
Average Case	θ(nk)
Worst Case	O(nk)

• Best Case Complexity - It occurs when there is no sorting required, i.e. the array is already sorted. The best-case time complexity of Radix sort is Ω(n+k).
• Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of Radix sort is θ(nk).
• Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of Radix sort is O(nk).

Radix sort is a non-comparative sorting algorithm that is better than the comparative sorting algorithms. It has linear time complexity that is better than the comparative algorithms with complexity O(n logn).

2. Space Complexity

Space Complexity	O(n + k)
Stable	YES

• The space complexity of Radix sort is O(n + k).

Implementation of Radix sort

Now, let's see the programs of Radix sort in different programming languages.

Program: Write a program to implement Radix sort in C language.

#include <stdio.h>  
  
int getMax(int a[], int n) {  
   int max = a[0];  
   for(int i = 1; i<n; i++) {  
      if(a[i] > max)  
         max = a[i];  
   }  
   return max; //maximum element from the array  
}  
  
void countingSort(int a[], int n, int place) // function to implement counting sort  
{  
  int output[n + 1];  
  int count[10] = {0};    
  
  // Calculate count of elements  
  for (int i = 0; i < n; i++)  
    count[(a[i] / place) % 10]++;  
      
  // Calculate cumulative frequency  
  for (int i = 1; i < 10; i++)  
    count[i] += count[i - 1];  
  
  // Place the elements in sorted order  
  for (int i = n - 1; i >= 0; i--) {  
    output[count[(a[i] / place) % 10] - 1] = a[i];  
    count[(a[i] / place) % 10]--;  
  }  
  
  for (int i = 0; i < n; i++)  
    a[i] = output[i];  
}  
  
// function to implement radix sort  
void radixsort(int a[], int n) {  
   
  // get maximum element from array  
  int max = getMax(a, n);  
  
  // Apply counting sort to sort elements based on place value  
  for (int place = 1; max / place > 0; place *= 10)  
    countingSort(a, n, place);  
}  
  
// function to print array elements  
void printArray(int a[], int n) {  
  for (int i = 0; i < n; ++i) {  
    printf("%d  ", a[i]);  
  }  
  printf("\n");  
}  
  
int main() {  
  int a[] = {181, 289, 390, 121, 145, 736, 514, 888, 122};  
  int n = sizeof(a) / sizeof(a[0]);  
  printf("Before sorting array elements are - \n");  
  printArray(a,n);  
  radixsort(a, n);  
  printf("After applying Radix sort, the array elements are - \n");  
  printArray(a, n);  
}  

Output:

After the execution of the above code, the output will be -