Prefix to Postfix and Postfix to Prefix

Conversion of Prefix to Postfix expression

Before understanding the conversion of prefix to postfix conversion, we should know about the prefix and postfix expressions separately.

What is Prefix conversion?

An infix expression is an expression in which the operators are written between the two operands. If we move the operator before the operands then it is known as a prefix expression. In other words, prefix expression can be defined as an expression in which all the operators precede the two operands.

For example:

If the infix expression is given as: A + B * C

As we know that the multiplication operator * has a higher precedence than the addition operator. First, multiplication operator will move before operand B shown as below:

A + * B C

Once the multiplication operator is moved before 'B' operand, addition operator will move before the operand 'A' shown as below:

+ A * B C

Evaluation of Prefix Expression using Stack

Step 1: Initialize a pointer 'S' pointing to the end of the expression.

Step 2: If the symbol pointed by 'S' is an operand then push it into the stack.

Step 3: If the symbol pointed by 'S' is an operator then pop two operands from the stack. Perform the operation on these two operands and stores the result into the stack.

Step 4: Decrement the pointer 'S' by 1 and move to step 2 as long as the symbols left in the expression.

Step 5: The final result is stored at the top of the stack and return it.

Step 6: End

Let's understand the evaluation of prefix expression through an example.

Expression: +, -, *, 2, 2, /, 16, 8, 5

First, we will reverse the expression given above.

Expression: 5, 8, 16, /, 2, 2, *, -, +

We will use the stack data structure to evaluate the prefix expression.

Symbol Scanned	Stack
5	5
8	5, 8
16	5, 8, 16
/	5, 2
2	5, 2, 2
2	5, 2, 2, 2
*	5, 2, 4
-	5, 2
+	7

The final result of the above expression is 7.

What is Postfix expression?

If we move the operators after the operands then it is known as a postfix expression. In other words, postfix expression can be defined as an expression in which all the operators are present after the operands.

For example:

If the infix expression is A + B * C

As we know that the multiplication operator has a higher precedence than the addition operator, so multiplication operator will move after the operands B and C shown as below:

A + B C *

Once the multiplication operator is moved after the operand C, then the addition operator will come after the multiplication operator shown as below:

A B C * +

Evaluation of Postfix expression using Stack

Algorithm for the evaluation of postfix expression using stack:

Step 1: Create an empty stack used for storing the operands.

Step 2: Scan each element of an expression one be one and do the following:

• If the element is an operand then push it into the stack.
• If the element is an operator then pop two operands from the stack. Perform operation on these operands. Push the final result into the stack.

Step 3: When the expression is scanned completely, the value available in the stack would be the final output of the given expression.

Let's understand the evaluation of postfix expression using stack through an example.

If the expression is: 5, 6, 2, +, *, 12, 4, /, -

Symbol Scanned	Stack
5	5
6	5, 6
2	5, 6, 2
+	5, 8
*	40
12	40, 12
4	40, 12, 4
/	40, 3
-	37

The result of the above expression is 37.

Conversion of Prefix to Postfix Expression

Here, we will see the conversion of prefix to postfix expression using a stack data structure.

Rules for prefix to postfix expression using stack data structure:

• Scan the prefix expression from right to left, i.e., reverse.
• If the incoming symbol is an operand then push it into the stack.
• If the incoming symbol is an operator then pop two operands from the stack. Once the operands are popped out from the stack, we add the incoming symbol after the operands. When the operator is added after the operands, then the expression is pushed back into the stack.
• Once the whole expression is scanned, pop and print the postfix expression from the stack.

Pseudocode for prefix to postfix conversion

Function PrefixToPostfix(string prefix)  
1.   Stack s  
2.   Loop: i = prefix.length-1 to 0  
•   if prefix[i] is operand ->  
s.push(prefix[i])  
•   else if prefix[i] is operator->  
op1 = s.top()  
s.pop()  
op2 = s.top()  
s.pop()  
exp = op1 + op2 + prefix[i]  
s.push(exp)  
End Loop  
3.   Return s.top

Let's understand the conversion of Prefix to Postfix expression using Stack through an example.

If the expression is: * - A / B C - / A K L

Symbols to be scanned	Action	Stack	Description
L	Push L into the stack	L
K	Push K into the stack	L, K
A	Push A into the stack	L, K, A
/	Pop A from the stack Pop K from the stack Push A K / into the stack	L, A K /	Pop two operands from the stack, i.e., A and K. Add '/' operator after K operand, i.e., AK/. Push AK/ into the stack.
-	Pop A K / and L from the stack. Push (A K / L -) into the stack	A K / L -	Pop two operands from the stack, i.e., AK/ and L. Add '-' operator after 'L' operand.
C	Push C into the stack	AK/L-, C
B	Push B into the stack	AK/L-, C, B
/	Pop B and C from the stack. Push BC/ into the stack.	AK/L-, BC/	Pop two operands from the stack, i.e., B and C. Add '/' operator after C operator, i.e., BC/. Push BC/ into the stack.
A	Push A into the stack	AK/L-, BC/, A
-	Pop BC/ and A from the stack. Push ABC/- into the stack.	AK/L-, ABC/-	Pop two operands from the stack, i.e., A and BC/. Add '-' operator after '/'.
*	Pop ABC/- and AK/L- from the stack. Push ABC/AK/L-* into the stack.	ABC/-AK/L-*	Pop two operands from the stack, i.e., ABC/-, and AK/L- . Add '*' operator after L and '-' operator, i.e., ABC/-AK/L-*.

Conversion of Postfix to Prefix expression

What is Postfix expression?

A postfix expression is said to be an expression in which the operator appears after the operands. It can be written as:

(operand) (operand) (operator)

For example:

If the expression is:

(A+B) * (C+D)

Firstly, operator precedence rules will be applied to the above expression. Since the parenthesis has higher precedence than the multiplication operator; therefore '+' will be resolved first, and the + operator will come after AB and CD shown as below:

(AB+) * (CD+)

Now, the multiplication operator will move after CD+ shown as below:

AB+ CD+*

What is Prefix Expression?

A prefix expression is said to be an expression in which the operator appears before the operands.

For example:

If the expression is given as:

(A+B) * (C+D)

Firstly, operator precedence rules will be applied to the above expression. Since the parenthesis has higher precedence than the multiplication operator; therefore, the '+' operator will be resolved first, and the '+' operator will move before the operands AB and CD shown as below:

(+AB) * (+CD)

Now, the multiplication operator will move before the +AB shown as below:

*+AB+CD

Conversion of Postfix to Prefix expression

There are two ways of converting a postfix into a prefix expression:

1. Conversion of Postfix to Prefix expression manually.
2. Conversion of Postfix to Prefix expression using stack.

Conversion of Postfix to Prefix expression manually

The following are the steps required to convert postfix into prefix expression:

• Scan the postfix expression from left to right.
• Select the first two operands from the expression followed by one operator.
• Convert it into the prefix format.
• Substitute the prefix sub expression by one temporary variable
• Repeat this process until the entire postfix expression is converted into prefix expression.

Let's understand through an example.

a b - c +

First, we scan the expression from left to right. We will move '-' operator before the operand ab.

-abc+

The next operator '+' is moved before the operand -abc is shown as below:

+-abc

Conversion of Postfix to Prefix expression using Stack

The following are the steps used to convert postfix to prefix expression using stack:

• Scan the postfix expression from left to right.
• If the element is an operand, then push it into the stack.
• If the element is an operator, then pop two operands from the stack.

Create an expression by concatenating two operands and adding operator before the operands.

Push the result back to the stack.

• Repeat the above steps until we reach the end of the postfix expression.

Pseudocode for the conversion of Postfix to Prefix

Function PostfixToPrefix(string postfix)  

1.  Stack s  

2.  Loop: i = 0 to postfix.length  

2.1 if postfix[i] is operand ->  

s.push(postfix[i])  

  

2.2 else if postfix[i] is operator->  

op1 = s.top()  

s.pop()  

op2 = s.top()  

s.pop()  

expression = postfix[i] + op2 + op1  

s.push(expression)  

          end loop  

         return s.top  

Let's understand the conversion of postfix to prefix expression using stack.

If the Postfix expression is given as:

AB + CD - *

Symbol Scanned	Action	Stack	Description
A	Push A into the stack	A
B	Push B into the stack	AB
+	Pop B from the stack Pop A from the stack Push +AB into the stack.	+AB	Pop two operands from the stack, i.e., A and B. Add '+' operator before the operands AB, i.e., +AB.
C	Push C into the stack	+ABC
D	Push D into the stack	+ABCD
-	Pop D from the stack. Pop C from the stack. Push -CD into the stack	+AB -CD	Pop two operands from the stack, i.e., D and C. Add '-' operator before the operands CD, i.e., -CD.
*	Pop -CD from the stack. Pop +AB from the stack. Push *+AB -CD into the stack.	*+AB - CD	Pop two operands from the stack, i.e., -CD and +AB. Add '*' operator before +AB then the expression would become *+AB-CD.

The prefix expression of the above postfix expression is *+AB-CD.

Implementation of Postfix to Prefix conversion in C++

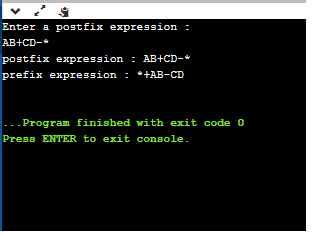
// C++ program to convert postfix to prefix expression.  

#include <iostream>  

#include<stack>  

using namespace std;  

// Checking whether the symbol is operand or not..  

bool isOperand(char c)  

{  

    if((c>='a' && c<='z') || (c>='A' && c<='Z'))  

    {  

        return true;  

    }  

    else  

    {  

        return false;  

    }  

}  

// Converting postfix to prefix expression in C++  

string postfixtoprefix(string postfix)  

{  

    stack<string> s;  // using predefined stack data structure in stl library  

   //  executing the loop from 0 till the length of the expression..  

   for(int i=0; i< postfix.length(); i++)  

    {  

        if(isOperand(postfix[i]))  // calling the isOperand() function  

        {  

            string op(1, postfix[i]);  // converting the char type variable into string type.  

            s.push(op);  // Pushing the operand into the stack..  

        }  

        else  

        {  

            string op1 = s.top();  // declaration of op1 variable of type string.  

            s.pop(); // pop the operand from the stack.  

            string op2 = s.top(); // declaration of op2 variable of type string  

            s.pop(); // pop the operand from the stack.  

            string expression = postfix[i] + op2 + op1;  // concatenating the operands and operator  

            s.push(expression); // push the expression into the stack.  

              

        }  

          

    }  

    return s.top(); // returning the top of the stack.  

}  

int main()  

{  

    string postfix, prefix; // declaration of two variables of type string  

    std::cout << "Enter a postfix expression :" << std::endl;  

    std::cin >> postfix;  

    std::cout << "postfix expression : " << postfix<<std::endl;  

    prefix = postfixtoprefix(postfix); // calling the postfixtoprefix() function  

    std::cout << "prefix expression : " << prefix<< std::endl;  

    return 0;  

}

Output