Single Source Shortest Paths

Introduction:

In a shortest- paths problem, we are given a weighted, directed graphs G = (V, E), with weight function w: E → R mapping edges to real-valued weights. The weight of path p = (v₀,v₁,..... v_k) is the total of the weights of its constituent edges:

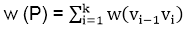
We define the shortest - path weight from u to v by δ(u,v) = min (w (p): u→v), if there is a path from u to v, and δ(u,v)= ∞, otherwise.

The shortest path from vertex s to vertex t is then defined as any path p with weight w (p) = δ(s,t).

The breadth-first- search algorithm is the shortest path algorithm that works on unweighted graphs, that is, graphs in which each edge can be considered to have unit weight.

In a Single Source Shortest Paths Problem, we are given a Graph G = (V, E), we want to find the shortest path from a given source vertex s ∈ V to every vertex v ∈ V.

Variants:

There are some variants of the shortest path problem.

• Single- destination shortest - paths problem: Find the shortest path to a given destination vertex t from every vertex v. By shift the direction of each edge in the graph, we can shorten this problem to a single - source problem.
• Single - pair shortest - path problem: Find the shortest path from u to v for given vertices u and v. If we determine the single - source problem with source vertex u, we clarify this problem also. Furthermore, no algorithms for this problem are known that run asymptotically faster than the best single - source algorithms in the worst case.
• All - pairs shortest - paths problem: Find the shortest path from u to v for every pair of vertices u and v. Running a single - source algorithm once from each vertex can clarify this problem; but it can generally be solved faster, and its structure is of interest in the own right.

Shortest Path: Existence:

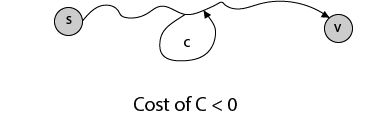
If some path from s to v contains a negative cost cycle then, there does not exist the shortest path. Otherwise, there exists a shortest s - v that is simple.