Bubble sort Algorithm

Bubble sort works on the repeatedly swapping of adjacent elements until they are not in the intended order. It is called bubble sort because the movement of array elements is just like the movement of air bubbles in the water. Bubbles in water rise up to the surface; similarly, the array elements in bubble sort move to the end in each iteration.

Although it is simple to use, it is primarily used as an educational tool because the performance of bubble sort is poor in the real world. It is not suitable for large data sets. The average and worst-case complexity of Bubble sort is O(n²), where n is a number of items.

Bubble short is majorly used where -

complexity does not matter
simple and shortcode is preferred

Algorithm

In the algorithm given below, suppose arr is an array of n elements. The assumed swap function in the algorithm will swap the values of given array elements.

begin BubbleSort(arr)
for all array elements
  if arr[i] > arr[i+1]
swap(arr[i], arr[i+1])
end if
end for
return arr
end BubbleSort

Working of Bubble sort Algorithm

Now, let's see the working of Bubble sort Algorithm.

To understand the working of bubble sort algorithm, let's take an unsorted array. We are taking a short and accurate array, as we know the complexity of bubble sort is O(n²).

Let the elements of array are -

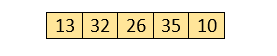
First Pass

Sorting will start from the initial two elements. Let compare them to check which is greater.

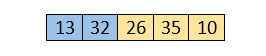
Here, 32 is greater than 13 (32 > 13), so it is already sorted. Now, compare 32 with 26.

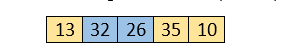
Here, 26 is smaller than 36. So, swapping is required. After swapping new array will look like -

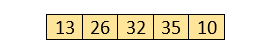
Now, compare 32 and 35.

Here, 35 is greater than 32. So, there is no swapping required as they are already sorted.

Now, the comparison will be in between 35 and 10.

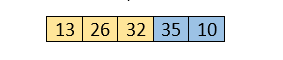
Here, 10 is smaller than 35 that are not sorted. So, swapping is required. Now, we reach at the end of the array. After first pass, the array will be -

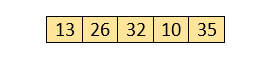
Now, move to the second iteration.

Second Pass

The same process will be followed for second iteration.

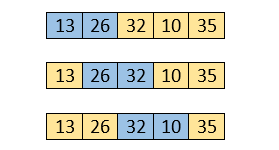
Here, 10 is smaller than 32. So, swapping is required. After swapping, the array will be -

Now, move to the third iteration.

Third Pass

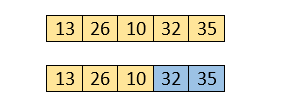
The same process will be followed for third iteration.

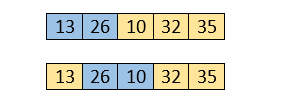
Here, 10 is smaller than 26. So, swapping is required. After swapping, the array will be -

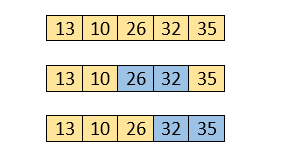
Now, move to the fourth iteration.

Fourth pass

Similarly, after the fourth iteration, the array will be -

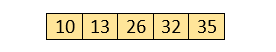
Hence, there is no swapping required, so the array is completely sorted.

Bubble sort complexity

Now, let's see the time complexity of bubble sort in the best case, average case, and worst case. We will also see the space complexity of bubble sort.

1. Time Complexity

Case	Time Complexity
Best Case	O(n)
Average Case	O(n²)
Worst Case	O(n²)

Best Case Complexity - It occurs when there is no sorting required, i.e. the array is already sorted. The best-case time complexity of bubble sort is O(n).
Average Case Complexity - It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of bubble sort is O(n²).
Worst Case Complexity - It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of bubble sort is O(n²).

2. Space Complexity

Space Complexity

O(1)

Stable

YES

The space complexity of bubble sort is O(1). It is because, in bubble sort, an extra variable is required for swapping.

The space complexity of optimized bubble sort is O(2). It is because two extra variables are required in optimized bubble sort.

Now, let's discuss the optimized bubble sort algorithm.

Optimized Bubble sort Algorithm

In the bubble sort algorithm, comparisons are made even when the array is already sorted. Because of that, the execution time increases.

To solve it, we can use an extra variable swapped. It is set to true if swapping requires; otherwise, it is set to false.

It will be helpful, as suppose after an iteration, if there is no swapping required, the value of variable swapped will be false. It means that the elements are already sorted, and no further iterations are required.

This method will reduce the execution time and also optimizes the bubble sort.

Algorithm for optimized bubble sort

Implementation of Bubble sort

Now, let's see the programs of Bubble sort in different programming languages.

Program: Write a program to implement bubble sort in C language.

#include<stdio.h>
void print(int a[], int n) //function to print array elements
{
  int i;
  for(i = 0; i < n; i++)
{
printf("%d ",a[i]);
}
}
void bubble(int a[], int n) // function to implement bubble sort
{
int i, j, temp;
for(i = 0; i < n; i++)
{
  for(j = i+1; j < n; j++)
{
  if(a[j] < a[i])
{
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
}
void main ()
{
  int i, j,temp;
  int a[5] = { 10, 35, 32, 13, 26};
  int n = sizeof(a)/sizeof(a[0]);
printf("Before sorting array elements are - \n");
print(a, n);
bubble(a, n);
printf("\nAfter sorting array elements are - \n");
print(a, n);
}

Output

Header Ads Widget

Bubble sort Algorithm

Algorithm