Skip list in Data structure

What is a skip list?

The skip list is a probabilisitc data structure that is built upon the general idea of a linked list. The skip list uses probability to build subsequent layers of linked lists upon an original linked list. Each additional layer of links contains fewer elements, but no new elements.

You can think about the skip list like a subway system. There's one train that stops at every single stop. However, there is also an express train. This train doesn't visit any unique stops, but it will stop at fewer stops. This makes the express train an attractive option if you know where it stops.

Skip lists are very useful when you need to be able to concurrently access your data structure. Imagine a red-black tree, an implementation of the binary search tree. If you insert a new node into the red-black tree, you might have to rebalance the entire thing, and you won't be able to access your data while this is going on. In a skip list, if you have to insert a new node, only the adjacent nodes will be affected, so you can still access large part of your data while this is happening.

Properties

A skip list starts with a basic, ordered, linked list. This list is sorted, but we can't do a binary search on it because it is a linked list and we cannot index into it. But the ordering will come in handy later.

Then, another layer is added on top of the bottom list. This new layer will include any given element from the previous layer with probability $�\mathrm{.}$ This probability can vary, but oftentimes $\frac{1}{2}$ is used. Additionally, the first node in the linked list is often always kept, as a header for the new layer. Take a look at the following graphics and see how some elements are kept but others are discarded. Here, it just so happened that half of the elements are kept in each new layer, but it could be more or less--it's all probabilistic. In all cases, each new layer is still ordered.

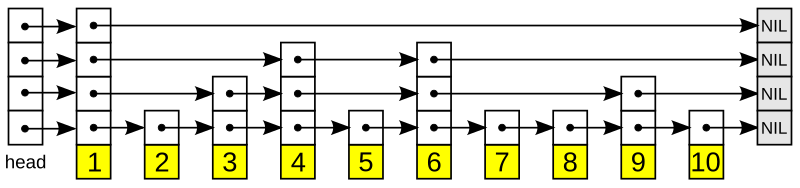An example implementation of a skip list

A skip list $�$ has a few important properties that are referenced in its analysis. It has a height of $ℎ$ which is the number of linked lists in it. It has a number of distinct elements, $�\mathrm{.}$ And it has a probability $�,$ which is usually $\frac{1}{2}\mathrm{.}$

The highest element (one that appears in the most lists) will appear in  lists, on average--we'll prove this later. This, if we use $�=\frac{1}{2}$, there are  lists. This is the average value of $ℎ$. Another way of saying "Every element in a linked list is in the linked list below it" is "Every element in level ${�}_{�+1}$ exists in level ${�}_{�}\mathrm{.}$"

Each element in the skip list has four pointers. It points to the node to its left, its right, its top, and its bottom. These quad-nodes will allow us to efficiently search through the skip list.

Skip list structure

It is built in two layers: The lowest layer and Top layer.

The lowest layer of the skip list is a common sorted linked list, and the top layers of the skip list are like an "express line" where the elements are skipped.

Complexity table of the Skip list

S. No	Complexity	Average case	Worst case
1.	Access complexity	O(logn)	O(n)
2.	Search complexity	O(logn)	O(n)
3.	Delete complexity	O(logn)	O(n)
4.	Insert complexity	O(logn)	O(n)
5.	Space complexity	-	O(nlogn)

Working of the Skip list

Let's take an example to understand the working of the skip list. In this example, we have 14 nodes, such that these nodes are divided into two layers, as shown in the diagram.

The lower layer is a common line that links all nodes, and the top layer is an express line that links only the main nodes, as you can see in the diagram.

Suppose you want to find 47 in this example. You will start the search from the first node of the express line and continue running on the express line until you find a node that is equal a 47 or more than 47.

You can see in the example that 47 does not exist in the express line, so you search for a node of less than 47, which is 40. Now, you go to the normal line with the help of 40, and search the 47, as shown in the diagram.

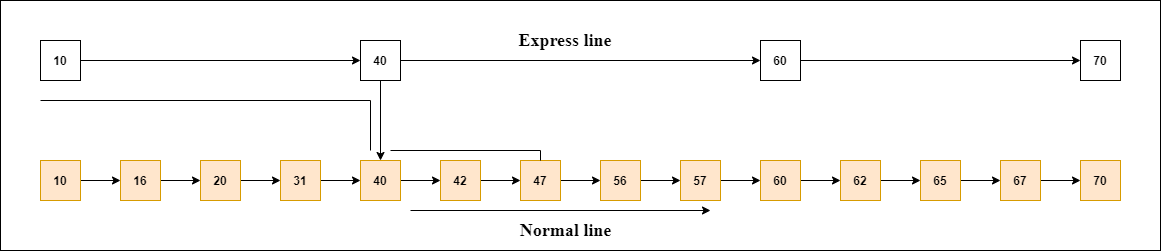
Note: Once you find a node like this on the "express line", you go from this node to a "normal lane" using a pointer, and when you search for the node in the normal line.

Skip List Basic Operations

There are the following types of operations in the skip list.

• Insertion operation: It is used to add a new node to a particular location in a specific situation.
• Deletion operation: It is used to delete a node in a specific situation.
• Search Operation: The search operation is used to search a particular node in a skip list.

Algorithm of the insertion operation

Insert(key)
    p = Search(key)
    q = null
    i = 1
    repeat
        i = i + 1                   //Height of tower for new element
        if i >= h
            h = h + 1
            createNewLevel()        //Creates new linked list level
        while (p.above == null)
            p = p.prev              //Scan backwards until you can go up
        p = p.above
        q = insertAfter(key, p)     //Insert our key after position p
    until CoinFlip() == 'Tails'
    n = n + 1
    return q

First, we always insert the key into the bottom list at the correct location. Then, we have to promote the new element. We do so by flipping a fair coin. If it comes up heads, we promote the new element. By flipping this fair coin, we are essentially deciding how big to make the tower for the new element. We scan backwards from our position until we can go up, and then we go up a level and insert our key right after our current position.

While we are flipping our coin, if the number of heads starts to grow larger than our current height, we have to make sure to create new levels in our skip list to accommodate this. Lines 7-9 of this function take care of that for us.

Algorithm of deletion operation

Delete(key)
    Search for all positions p_0, ..., p_i where key exists
    if none are found
        return
    Delete all positions p_0, ..., p_i
    Remove all empty layers of skip list

Algorithm of searching operation

Search(key)
    p = top-left node in S
    while (p.below != null) do        //Scan down
        p = p.below
        while (key >= p.next) do      //Scan forward
            p = p.next
    return p

Height of the Skip List

Earlier, we said that there will be  lists in total. But why? If each newly created level is done so probabilistically, how can we know that?

The probability ${�}_{�}$ that an element in skip list $�$ with $�$ total elements gets up to level $�$ is just

${�}_{�}=\frac{1}{2^{�}}$

because if the probability is $\frac{1}{2},$ then to create a new level, we're tossing a coin for each element to see if it should be included. So, the probability that at least one of the $�$ elements gets to level $�$ is

${�}_{�}\le \frac{�}{2^{�}}\mathrm{.}$

Let's try some numbers to see what this means. If  then

If $�$ increases slightly to , then

This means, that if $�=1000$, there is one in a million chance of any one particular element making it to the top layer. This analysis, of course, is not strict, but with a high probability (a word used often in randomized algorithms), $�$ has a height of .

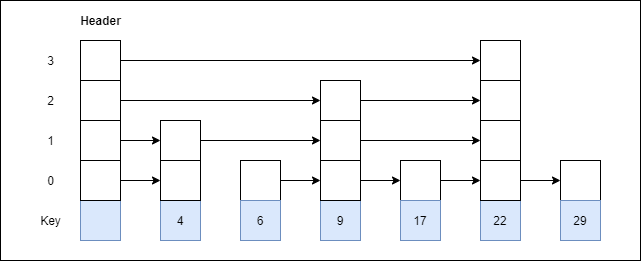
Example 1: Create a skip list, we want to insert these following keys in the empty skip list.

1. 6 with level 1.
2. 29 with level 1.
3. 22 with level 4.
4. 9 with level 3.
5. 17 with level 1.
6. 4 with level 2.

Ans:

Step 1: Insert 6 with level 1

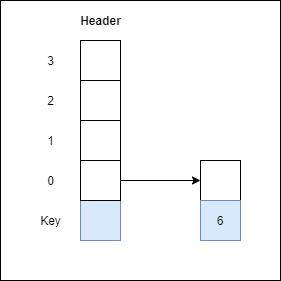
Step 2: Insert 29 with level 1

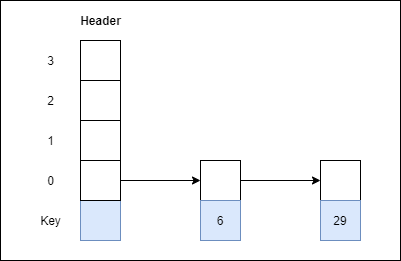
Step 3: Insert 22 with level 4

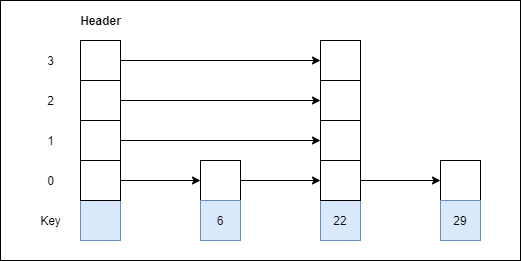
Step 4: Insert 9 with level 3

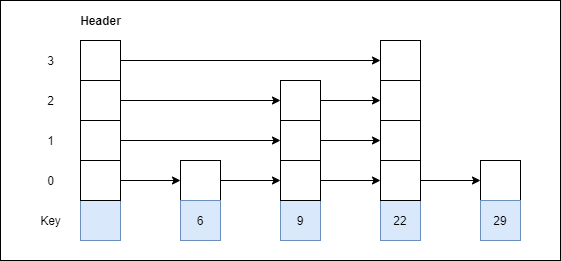
Step 5: Insert 17 with level 1

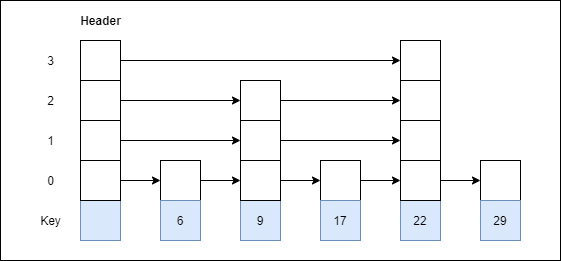
Step 6: Insert 4 with level 2

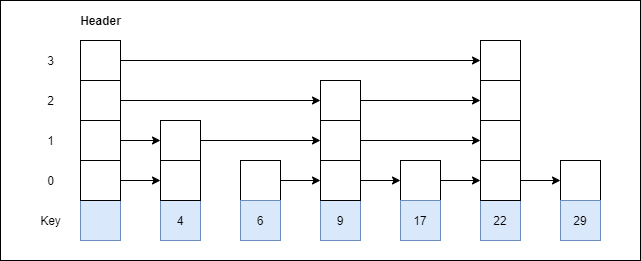
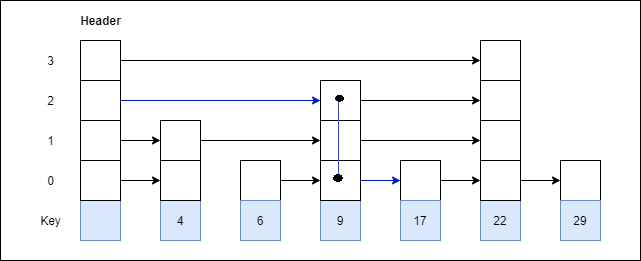
Example 2: Consider this example where we want to search for key 17.

Ans:

Advantages of the Skip list

1. If you want to insert a new node in the skip list, then it will insert the node very fast because there are no rotations in the skip list.
2. The skip list is simple to implement as compared to the hash table and the binary search tree.
3. It is very simple to find a node in the list because it stores the nodes in sorted form.
4. The skip list algorithm can be modified very easily in a more specific structure, such as indexable skip lists, trees, or priority queues.
5. The skip list is a robust and reliable list.

Disadvantages of the Skip list

1. It requires more memory than the balanced tree.
2. Reverse searching is not allowed.
3. The skip list searches the node much slower than the linked list.

Applications of the Skip list

1. It is used in distributed applications, and it represents the pointers and system in the distributed applications.
2. It is used to implement a dynamic elastic concurrent queue with low lock contention.
3. It is also used with the QMap template class.
4. The indexing of the skip list is used in running median problems.
5. The skip list is used for the delta-encoding posting in the Lucene search.