ID3 algorithm

ID3 algorithm

The steps in ID3 algorithm are as follows:

1. Calculate entropy for dataset.
2. For each attribute/feature.

2.1. Calculate entropy for all its categorical values.

2.2. Calculate information gain for the feature.

3. Find the feature with maximum information gain.
4. Repeat it until we get the desired tree.

 

Use ID3 algorithm on a data

We'll discuss it here mathematically and later see it's implementation in Python.
So, Let's take an example to make it more clear.

Day	Outlook	Temperature	Humidity	Wind	PlayTennis
D1	Sunny	Hot	High	Weak	No
D2	Sunny	Hot	High	Strong	No
D3	Overcast	Hot	High	Weak	Yes
D4	Rain	Mild	High	Weak	Yes
D5	Rain	Cool	Normal	Weak	Yes
D6	Rain	Cool	Normal	Strong	No
D7	Overcast	Cool	Normal	Strong	Yes
D8	Sunny	Mild	High	Weak	No
D9	Sunny	Cool	Normal	Weak	Yes
D10	Rain	Mild	Normal	Weak	Yes
D11	Sunny	Mild	Normal	Strong	Yes
D12	Overcast	Mild	High	Strong	Yes
D13	Overcast	Hot	Normal	Weak	Yes
D14	Rain	Mild	High	Strong	No

 

Here,dataset is of binary classes(yes and no), where 9 out of 14 are "yes" and 5 out of 14 are "no".

Complete entropy of dataset is:

H(S) = - p(yes) * log2(p(yes)) - p(no) * log2(p(no))

     = - (9/14) * log2(9/14) - (5/14) * log2(5/14)

     = - (-0.41) - (-0.53)

     = 0.94

 

For each attribute of the dataset, let's follow the step-2 of pseudocode : -

First Attribute - Outlook

Categorical values - sunny, overcast and rain

H(Outlook=sunny) = -(2/5)*log(2/5)-(3/5)*log(3/5) =0.971

H(Outlook=rain) = -(3/5)*log(3/5)-(2/5)*log(2/5) =0.971

H(Outlook=overcast) = -(4/4)*log(4/4)-0 = 0

 

Average Entropy Information for Outlook –

I(Outlook) = p(sunny) * H(Outlook=sunny) + p(rain) * H(Outlook=rain) + p(overcast) * H(Outlook=overcast)

= (5/14)*0.971 + (5/14)*0.971 + (4/14)*0

= 0.693

 

Information Gain = H(S) - I(Outlook)

                 = 0.94 - 0.693

                 = 0.247

 

Second Attribute - Temperature

Categorical values - hot, mild, cool

H(Temperature=hot) = -(2/4)*log(2/4)-(2/4)*log(2/4) = 1

H(Temperature=cool) = -(3/4)*log(3/4)-(1/4)*log(1/4) = 0.811

H(Temperature=mild) = -(4/6)*log(4/6)-(2/6)*log(2/6) = 0.9179

Average Entropy Information for Temperature -

I(Temperature) = p(hot)*H(Temperature=hot) + p(mild)*H(Temperature=mild) + p(cool)*H(Temperature=cool)

= (4/14)*1 + (6/14)*0.9179 + (4/14)*0.811

= 0.9108

 

Information Gain = H(S) - I(Temperature)

                 = 0.94 - 0.9108

                 = 0.0292

 

Third Attribute - Humidity

Categorical values - high, normal

H(Humidity=high) = -(3/7)*log(3/7)-(4/7)*log(4/7) = 0.983

H(Humidity=normal) = -(6/7)*log(6/7)-(1/7)*log(1/7) = 0.591

 

Average Entropy Information for Humidity -

I(Humidity) = p(high)*H(Humidity=high) + p(normal)*H(Humidity=normal)

= (7/14)*0.983 + (7/14)*0.591

= 0.787

 

Information Gain = H(S) - I(Humidity)

                 = 0.94 - 0.787

                 = 0.153

 

Fourth Attribute - Wind

Categorical values - weak, strong

H(Wind=weak) = -(6/8)*log(6/8)-(2/8)*log(2/8) = 0.811

H(Wind=strong) = -(3/6)*log(3/6)-(3/6)*log(3/6) = 1

 

Average Entropy Information for Wind -

I(Wind) = p(weak)*H(Wind=weak) + p(strong)*H(Wind=strong)

= (8/14)*0.811 + (6/14)*1

= 0.892

 

Information Gain = H(S) - I(Wind)

                 = 0.94 - 0.892

                 = 0.048

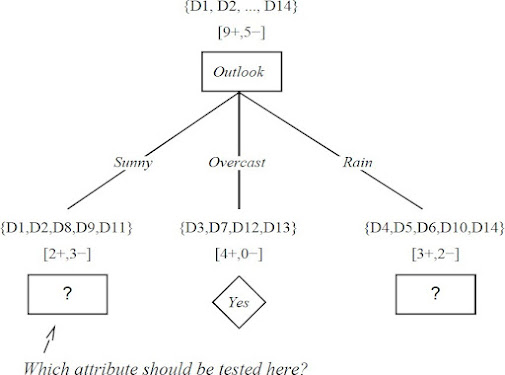
Here, the attribute with maximum information gain is Outlook. So, the decision tree built so far -

Here, when Outlook == overcast, it is of pure class(Yes).

Now, we have to repeat same procedure for the data with rows consist of Outlook value as Sunny and then for Outlook value as Rain.

Now, finding the best attribute for splitting the data with Outlook=Sunny values{ Dataset rows = [1, 2, 8, 9, 11]}.

Complete entropy of Sunny is -

H(S) = - p(yes) * log2(p(yes)) - p(no) * log2(p(no))

     = - (2/5) * log2(2/5) - (3/5) * log2(3/5)

     = 0.971

 

First Attribute - Temperature

Categorical values - hot, mild, cool

H(Sunny, Temperature=hot) = -0-(2/2)*log(2/2) = 0

H(Sunny, Temperature=cool) = -(1)*log(1)- 0 = 0

H(Sunny, Temperature=mild) = -(1/2)*log(1/2)-(1/2)*log(1/2) = 1

Average Entropy Information for Temperature -

I(Sunny, Temperature) = p(Sunny, hot)*H(Sunny, Temperature=hot) + p(Sunny, mild)*H(Sunny, Temperature=mild) + p(Sunny, cool)*H(Sunny, Temperature=cool)

= (2/5)*0 + (1/5)*0 + (2/5)*1

= 0.4

 

Information Gain = H(Sunny) - I(Sunny, Temperature)

                 = 0.971 - 0.4

                 = 0.571

 

Second Attribute - Humidity

Categorical values - high, normal

H(Sunny, Humidity=high) = - 0 - (3/3)*log(3/3) = 0

H(Sunny, Humidity=normal) = -(2/2)*log(2/2)-0 = 0

 

Average Entropy Information for Humidity -

I(Sunny, Humidity) = p(Sunny, high)*H(Sunny, Humidity=high) + p(Sunny, normal)*H(Sunny, Humidity=normal)

= (3/5)*0 + (2/5)*0

= 0

 

Information Gain = H(Sunny) - I(Sunny, Humidity)

                 = 0.971 - 0

                 = 0.971

 

Third Attribute - Wind

Categorical values - weak, strong

H(Sunny, Wind=weak) = -(1/3)*log(1/3)-(2/3)*log(2/3) = 0.918

H(Sunny, Wind=strong) = -(1/2)*log(1/2)-(1/2)*log(1/2) = 1

 

Average Entropy Information for Wind -

I(Sunny, Wind) = p(Sunny, weak)*H(Sunny, Wind=weak) + p(Sunny, strong)*H(Sunny, Wind=strong)

= (3/5)*0.918 + (2/5)*1

= 0.9508

 

Information Gain = H(Sunny) - I(Sunny, Wind)

                 = 0.971 - 0.9508

                 = 0.0202

 

Here, the attribute with maximum information gain is Humidity. So, the decision tree built so far -    

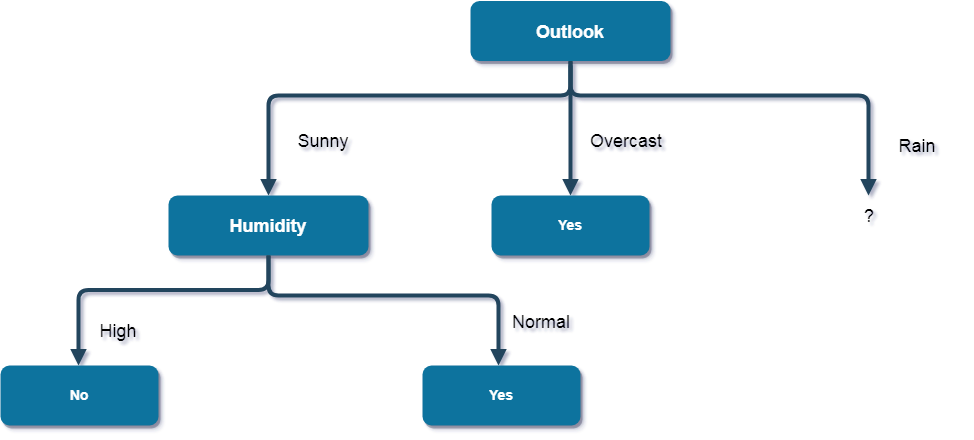
Here, when Outlook = Sunny and Humidity = High, it is a pure class of category "no". And When Outlook = Sunny and Humidity = Normal, it is again a pure class of category "yes". Therefore, we don't need to do further calculations.

Now, finding the best attribute for splitting the data with Outlook=Sunny values{ Dataset rows = [4, 5, 6, 10, 14]}.

Complete entropy of Rain is -

H(S) = - p(yes) * log2(p(yes)) - p(no) * log2(p(no))

     = - (3/5) * log(3/5) - (2/5) * log(2/5)

     = 0.971

 

First Attribute - Temperature

Categorical values - mild, cool

H(Rain, Temperature=cool) = -(1/2)*log(1/2)- (1/2)*log(1/2) = 1

H(Rain, Temperature=mild) = -(2/3)*log(2/3)-(1/3)*log(1/3) = 0.918

Average Entropy Information for Temperature -

I(Rain, Temperature) = p(Rain, mild)*H(Rain, Temperature=mild) + p(Rain, cool)*H(Rain, Temperature=cool)

= (2/5)*1 + (3/5)*0.918

= 0.9508

 

Information Gain = H(Rain) - I(Rain, Temperature)

                 = 0.971 - 0.9508

                 = 0.0202

 

Second Attribute - Wind

Categorical values - weak, strong

H(Wind=weak) = -(3/3)*log(3/3)-0 = 0

H(Wind=strong) = 0-(2/2)*log(2/2) = 0

 

Average Entropy Information for Wind -

I(Wind) = p(Rain, weak)*H(Rain, Wind=weak) + p(Rain, strong)*H(Rain, Wind=strong)

= (3/5)*0 + (2/5)*0

= 0

 

Information Gain = H(Rain) - I(Rain, Wind)

                 = 0.971 - 0

                 = 0.971

Here, the attribute with maximum information gain is Wind. So, the decision tree built so far -

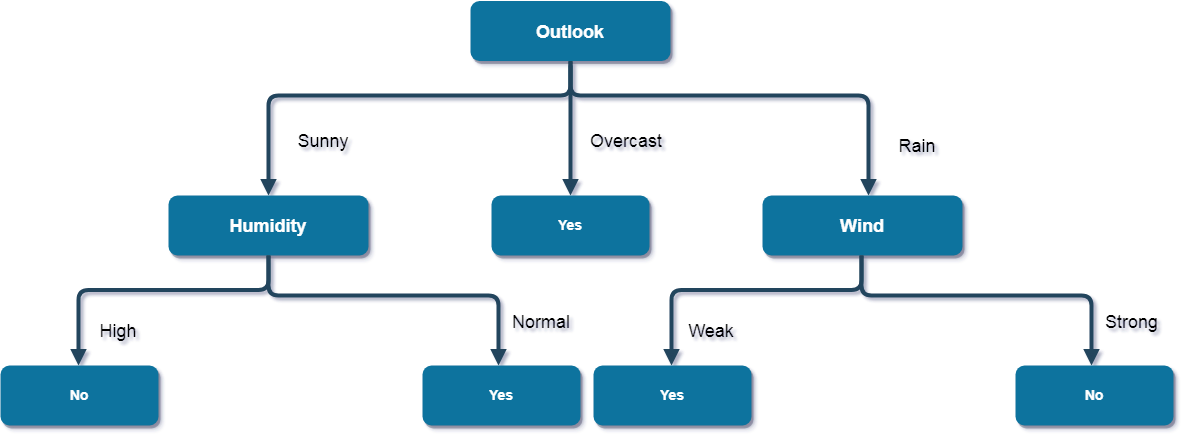Here, when Outlook = Rain and Wind = Strong, it is a pure class of category "no". And When Outlook = Rain and Wind = Weak, it is again a pure class of category "yes".

And this is our final desired tree for the given dataset.

 

What are the characteristics of ID3 algorithm?

Characteristics of ID3 Algorithm are as follows:

1. ID3 uses a greedy approach that's why it does not guarantee an optimal solution; it can get stuck in local optimums.
2. ID3 can overfit to the training data (to avoid overfitting, smaller decision trees should be preferred over larger ones).
3. This algorithm usually produces small trees, but it does not always produce the smallest possible tree.

ID3 is harder to use on continuous data (if the values of any given attribute is continuous, then there are many more places to split the data on this attribute, and searching for the best value to split by can be time consuming).