Markov Decision Process

Markov Decision Process

Markov Decision Process or MDP, is used to formalize the reinforcement learning problems. If the environment is completely observable, then its dynamic can be modeled as a Markov Process. In MDP, the agent constantly interacts with the environment and performs actions; at each action, the environment responds and generates a new state.

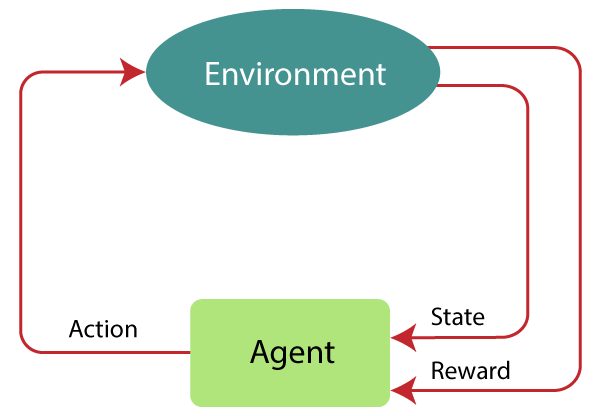
MDP is used to describe the environment for the RL, and almost all the RL problem can be formalized using MDP.

MDP contains a tuple of four elements (S, A, P_a, R_a):

• A set of finite States S
• A set of finite Actions A
• Rewards received after transitioning from state S to state S', due to action a.
• Probability P_a.

MDP uses Markov property, and to better understand the MDP, we need to learn about it.

Markov Property:

It says that "If the agent is present in the current state S1, performs an action a1 and move to the state s2, then the state transition from s1 to s2 only depends on the current state and future action and states do not depend on past actions, rewards, or states."

Or, in other words, as per Markov Property, the current state transition does not depend on any past action or state. Hence, MDP is an RL problem that satisfies the Markov property. Such as in a Chess game, the players only focus on the current state and do not need to remember past actions or states.

Finite MDP:

A finite MDP is when there are finite states, finite rewards, and finite actions. In RL, we consider only the finite MDP.

Markov Process:

Markov Process is a memoryless process with a sequence of random states S₁, S₂, ....., S_t that uses the Markov Property. Markov process is also known as Markov chain, which is a tuple (S, P) on state S and transition function P. These two components (S and P) can define the dynamics of the system.