Example of Reinforcement Learning in Practice

How does Reinforcement Learning Work?

To understand the working process of the RL, we need to consider two main things:

• Environment: It can be anything such as a room, maze, football ground, etc.
• Agent: An intelligent agent such as AI robot.

Let's take an example of a maze environment that the agent needs to explore. Consider the below image:

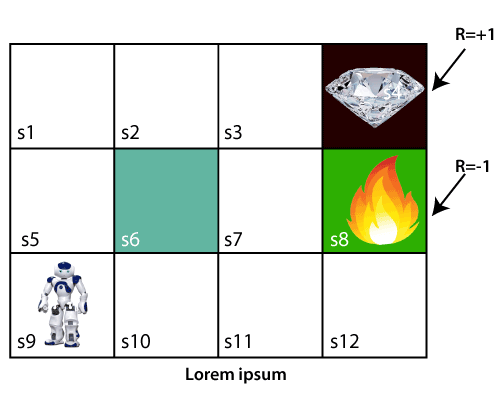
In the above image, the agent is at the very first block of the maze. The maze is consisting of an S₆ block, which is a wall, S₈ a fire pit, and S₄ a diamond block.

The agent cannot cross the S₆ block, as it is a solid wall. If the agent reaches the S₄ block, then get the +1 reward; if it reaches the fire pit, then gets -1 reward point. It can take four actions: move up, move down, move left, and move right.

The agent can take any path to reach to the final point, but he needs to make it in possible fewer steps. Suppose the agent considers the path S9-S5-S1-S2-S3, so he will get the +1-reward point.

The agent will try to remember the preceding steps that it has taken to reach the final step. To memorize the steps, it assigns 1 value to each previous step. Consider the below step:

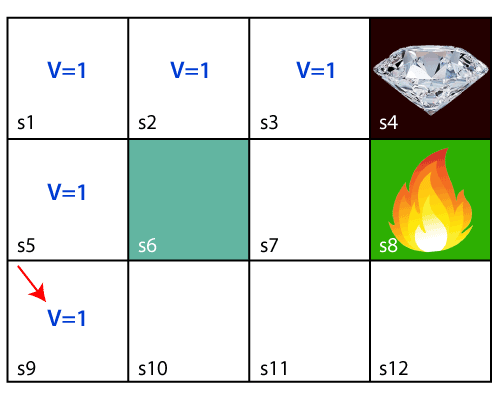
Now, the agent has successfully stored the previous steps assigning the 1 value to each previous block. But what will the agent do if he starts moving from the block, which has 1 value block on both sides? Consider the below diagram:

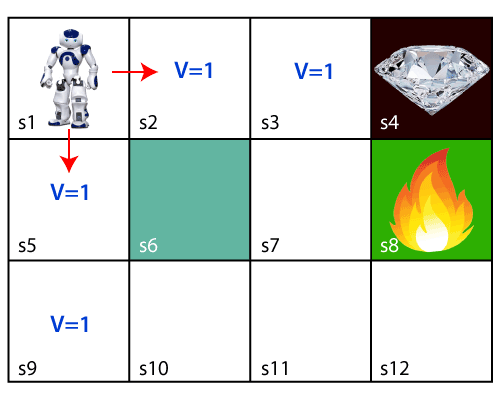
It will be a difficult condition for the agent whether he should go up or down as each block has the same value. So, the above approach is not suitable for the agent to reach the destination. Hence to solve the problem, we will use the Bellman equation, which is the main concept behind reinforcement learning.

The Bellman Equation

The Bellman equation was introduced by the Mathematician Richard Ernest Bellman in the year 1953, and hence it is called as a Bellman equation. It is associated with dynamic programming and used to calculate the values of a decision problem at a certain point by including the values of previous states.

It is a way of calculating the value functions in dynamic programming or environment that leads to modern reinforcement learning.

The key-elements used in Bellman equations are:

• Action performed by the agent is referred to as "a"
• State occurred by performing the action is "s."
• The reward/feedback obtained for each good and bad action is "R."
• A discount factor is Gamma "γ."

The Bellman equation can be written as:

1. V(s) = max [R(s,a) + γV(s`)]  

Where,

V(s)= value calculated at a particular point.

R(s,a) = Reward at a particular state s by performing an action.

γ = Discount factor

V(s`) = The value at the previous state.

In the above equation, we are taking the max of the complete values because the agent tries to find the optimal solution always.

So now, using the Bellman equation, we will find value at each state of the given environment. We will start from the block, which is next to the target block.

For 1st block:

V(s3) = max [R(s,a) + γV(s`)], here V(s')= 0 because there is no further state to move.

V(s3)= max[R(s,a)]=> V(s3)= max[1]=> V(s3)= 1.

For 2nd block:

V(s2) = max [R(s,a) + γV(s`)], here γ= 0.9(lets), V(s')= 1, and R(s, a)= 0, because there is no reward at this state.

V(s2)= max[0.9(1)]=> V(s)= max[0.9]=> V(s2) =0.9

For 3rd block:

V(s1) = max [R(s,a) + γV(s`)], here γ= 0.9(lets), V(s')= 0.9, and R(s, a)= 0, because there is no reward at this state also.

V(s1)= max[0.9(0.9)]=> V(s3)= max[0.81]=> V(s1) =0.81

For 4th block:

V(s5) = max [R(s,a) + γV(s`)], here γ= 0.9(lets), V(s')= 0.81, and R(s, a)= 0, because there is no reward at this state also.

V(s5)= max[0.9(0.81)]=> V(s5)= max[0.81]=> V(s5) =0.73

For 5th block:

V(s9) = max [R(s,a) + γV(s`)], here γ= 0.9(lets), V(s')= 0.73, and R(s, a)= 0, because there is no reward at this state also.

V(s9)= max[0.9(0.73)]=> V(s4)= max[0.81]=> V(s4) =0.66

Consider the below image:

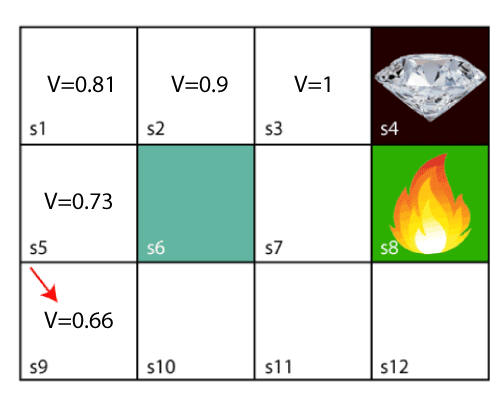
Now, we will move further to the 6^th block, and here agent may change the route because it always tries to find the optimal path. So now, let's consider from the block next to the fire pit.

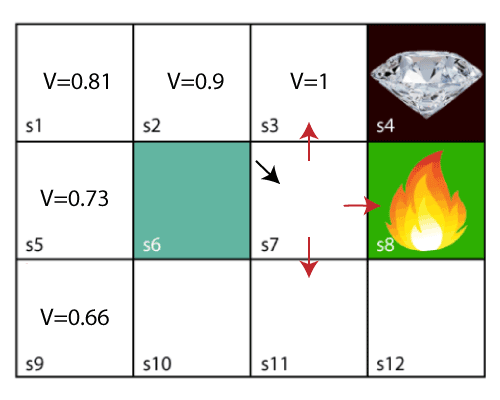
Now, the agent has three options to move; if he moves to the blue box, then he will feel a bump if he moves to the fire pit, then he will get the -1 reward. But here we are taking only positive rewards, so for this, he will move to upwards only. The complete block values will be calculated using this formula. Consider the below image:

---