Arden's Theorem

Arden's Theorem

You can use Arden’s Theorem to find out a regular expression of a Finite Automaton with the properties of regular expressions.

Statement −

Let’s assume that P and Q be two regular expressions.

Incase if P does not include a null string, then R = Q + RP has a unique solution that is R = QP*

Proof −

 [After putting the value R = Q + RP]

= Q + QP + RPP

If you include the value of R recursively repetitively then you will get the following equation −

It’s proved.

Assumptions for Applying Arden’s Theorem

• The transition diagram must not have NULL transitions
• It must have only one initial state

Method

Step 1 – Now create equations in the below mentioned form for all the states of the DFA having n states with initial state q1.

q1 = q1R11 + q2R21 + … + qnRn1 + ε

q2 = q1R12 + q2R22 + … + qnRn2

…………………………

…………………………

…………………………

…………………………

qn = q1R1n + q2R2n + … + qnRnn

Rij represents the set of labels of edges from qi to qj, if no such edge exists, then Rij = ∅

Step 2 − Solve these equations to get the equation for the final state in terms of Rij

Example:

Construct a regular expression corresponding to the automata given below −

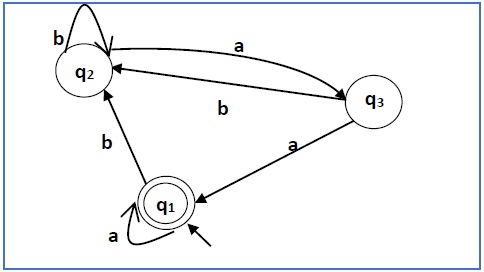
Solution −

Here the initial state and final state is q1.

The equations for the three states q1, q2, and q3 are as follows −

q1 = q1a + q3a + ε (ε move is because q1 is the initial state0

q2 = q1b + q2b + q3b

q3 = q2a

Now, we will solve these three equations −

q2 = q1b + q2b + q3b

= q1b + q2b + (q2a)b (Substituting value of q3)

= q1b + q2(b + ab)

= q1b (b + ab)* (Applying Arden’s Theorem)

q1 = q1a + q3a + ε

= q1a + q2aa + ε (Substituting value of q3)

= q1a + q1b(b + ab*)aa + ε (Substituting value of q2)

= q1(a + b(b + ab)*aa) + ε

= ε (a+ b(b + ab)*aa)*

= (a + b(b + ab)*aa)*

Hence, the regular expression is (a + b(b + ab)*aa)*.

Example:

Construct a regular expression corresponding to the automata given below −

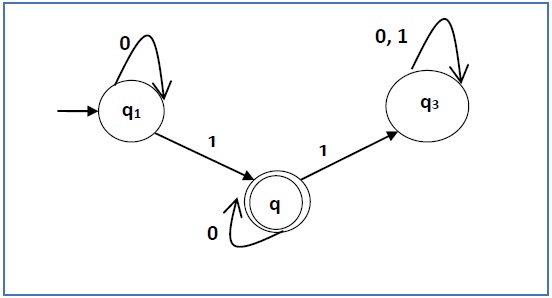
Solution −

Here the initial state is q1 and the final state is q2

Now we write down the equations −

q1 = q10 + ε

q2 = q11 + q20

q3 = q21 + q30 + q31

Now, we will solve these three equations −

q1 = ε0* [As, εR = R]

So, q1 = 0*

q2 = 0*1 + q20

So, q2 = 0*1(0)* [By Arden’s theorem]

Hence, the regular expression is 0*10*.

Example:

Construct the regular expression for the given DFA

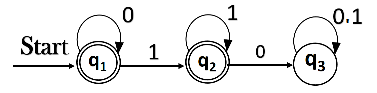
Solution:

Let us write down the equations

q1 = q1 0 + ε 

Since q1 is the start state, so ε will be added, and the input 0 is coming to q1 from q1 hence we write
State = source state of input × input coming to it

Similarly,

q2 = q1 1 + q2 1

q3 = q2 0 + q3 (0+1)

Since the final states are q1 and q2, we are interested in solving q1 and q2 only. Let us see q1 first

q1 =  q1 0 + ε

We can re-write it as

q1 = ε + q1 0

Which is similar to R = Q + RP, and gets reduced to R = OP*.

Assuming R = q1, Q = ε, P = 0

We get

q1 = ε.(0)*

q1 = 0*    (ε.R*= R*)

Substituting the value into q2, we will get

q2 = 0* 1 + q2 1

q2 = 0* 1 (1)*   (R = Q + RP  →  Q P*)

The regular expression is given by

r = q1 + q2

= 0^* + 0^* 1.1^*

r = 0^* + 0^* 1⁺    (1.1^* = 1⁺)

PROBLEMS BASED ON CONVERTING DFA TO REGULAR EXPRESSION-

 

Problem-01:

 

Find regular expression for the following DFA using Arden’s Theorem-

 

 

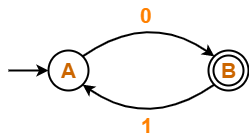
Solution-

 

Step-01:

 

Form a equation for each state-

• A = ∈ + B.1 ……(1)
• B = A.0 ……(2)

 

Step-02:

 

Bring final state in the form R = Q + RP.

 

Using (1) in (2), we get-

B = (∈ + B.1).0

B = ∈.0 + B.1.0

B = 0 + B.(1.0) ……(3)

 

Using Arden’s Theorem in (3), we get-

B = 0.(1.0)*

 

Thus, Regular Expression for the given DFA = 0(10)*

 

Problem-02:

 

Find regular expression for the following DFA using Arden’s Theorem-

 

 

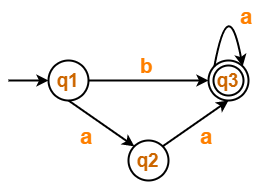
Solution-

 

Step-01:

 

Form a equation for each state-

• q1 = ∈ ……(1)
• q2 = q1.a ……(2)
• q3 = q1.b + q2.a + q3.a …….(3)

 

Step-02:

 

Bring final state in the form R = Q + RP.

 

Using (1) in (2), we get-

q2 = ∈.a

q2 = a …….(4)

 

Using (1) and (4) in (3), we get-

 

q3 = q1.b + q2.a + q3.a

q3 = ∈.b + a.a + q3.a

q3 = (b + a.a) + q3.a …….(5)

 

Using Arden’s Theorem in (5), we get-

q3 = (b + a.a)a*

 

Thus, Regular Expression for the given DFA = (b + aa)a*

 

Problem-03:

 

Find regular expression for the following DFA using Arden’s Theorem-

 

 

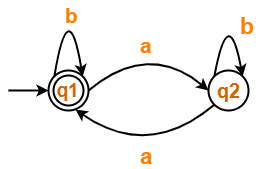
Solution-

 

Step-01:

 

Form a equation for each state-

• q1 = ∈ + q1.b + q2.a ……(1)
• q2 = q1.a + q2.b ……(2)

 

Step-02:

 

Bring final state in the form R = Q + RP.

 

Using Arden’s Theorem in (2), we get-

q2 = q1.a.b* …….(3)

 

Using (3) in (1), we get-

q1 = ∈ + q1.b + q1.a.b*.a

q1 = ∈ + q1.(b + a.b*.a) …….(4)

 

Using Arden’s Theorem in (4), we get-

q1 = ∈.(b + a.b*.a)*

q1 = (b + a.b*.a)*

 

Thus, Regular Expression for the given DFA = (b + a.b*.a)*

 

Problem-04:

 

Find regular expression for the following DFA using Arden’s Theorem-

 

 

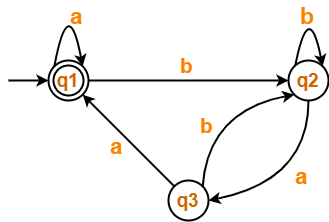
Solution-

 

Step-01:

 

Form a equation for each state-

• q1 = ∈ + q1.a + q3.a ……(1)
• q2 = q1.b + q2.b + q3.b ……(2)
• q3 = q2.a …….(3)

 

Step-02:

 

Bring final state in the form R = Q + RP.

 

Using (3) in (2), we get-

q2 = q1.b + q2.b + q2.a.b

q2 = q1.b + q2.(b + a.b) …….(4)

 

Using Arden’s Theorem in (4), we get-

q2 = q1.b.(b + a.b)* …….(5)

 

Using (5) in (3), we get-

q3 = q1.b.(b + a.b)*.a …….(6)

 

Using (6) in (1), we get-

q1 = ∈ + q1.a + q1.b.(b + a.b)*.a.a

q1 = ∈ + q1.(a + b.(b + a.b)*.a.a) …….(7)

 

Using Arden’s Theorem in (7), we get-

q1 = ∈.(a + b.(b + a.b)*.a.a)*

q1 = (a + b.(b + a.b)*.a.a)*

 

Thus, Regular Expression for the given DFA = (a + b(b + ab)*aa)*