Routing

Routing algorithm

• In order to transfer the packets from source to the destination, the network layer must determine the best route through which packets can be transmitted.
• Whether the network layer provides datagram service or virtual circuit service, the main job of the network layer is to provide the best route. The routing protocol provides this job.
• The routing protocol is a routing algorithm that provides the best path from the source to the destination. The best path is the path that has the "least-cost path" from source to the destination.
• Routing is the process of forwarding the packets from source to the destination but the best route to send the packets is determined by the routing algorithm.

Classification of a Routing algorithm

The Routing algorithm is divided into two categories:

• Adaptive Routing algorithm
• Non-adaptive Routing algorithm

---

Adaptive Routing algorithm

• An adaptive routing algorithm is also known as dynamic routing algorithm.
• This algorithm makes the routing decisions based on the topology and network traffic.
• The main parameters related to this algorithm are hop count, distance and estimated transit time.

An adaptive routing algorithm can be classified into three parts:

• Centralized algorithm: It is also known as global routing algorithm as it computes the least-cost path between source and destination by using complete and global knowledge about the network. This algorithm takes the connectivity between the nodes and link cost as input, and this information is obtained before actually performing any calculation. Link state algorithm is referred to as a centralized algorithm since it is aware of the cost of each link in the network.
• Isolation algorithm: It is an algorithm that obtains the routing information by using local information rather than gathering information from other nodes.
• Distributed algorithm: It is also known as decentralized algorithm as it computes the least-cost path between source and destination in an iterative and distributed manner. In the decentralized algorithm, no node has the knowledge about the cost of all the network links. In the beginning, a node contains the information only about its own directly attached links and through an iterative process of calculation computes the least-cost path to the destination. A Distance vector algorithm is a decentralized algorithm as it never knows the complete path from source to the destination, instead it knows the direction through which the packet is to be forwarded along with the least cost path.

---

Non-Adaptive Routing algorithm

• Non Adaptive routing algorithm is also known as a static routing algorithm.
• When booting up the network, the routing information stores to the routers.
• Non Adaptive routing algorithms do not take the routing decision based on the network topology or network traffic.

The Non-Adaptive Routing algorithm is of two types:

Flooding: In case of flooding, every incoming packet is sent to all the outgoing links except the one from it has been reached. The disadvantage of flooding is that node may contain several copies of a particular packet.

Random walks: In case of random walks, a packet sent by the node to one of its neighbors randomly. An advantage of using random walks is that it uses the alternative routes very efficiently.

Differences b/w Adaptive and Non-Adaptive Routing Algorithm

Basis Of Comparison	Adaptive Routing algorithm	Non-Adaptive Routing algorithm
Define	Adaptive Routing algorithm is an algorithm that constructs the routing table based on the network conditions.	The Non-Adaptive Routing algorithm is an algorithm that constructs the static table to determine which node to send the packet.
Usage	Adaptive routing algorithm is used by dynamic routing.	The Non-Adaptive Routing algorithm is used by static routing.
Routing decision	Routing decisions are made based on topology and network traffic.	Routing decisions are the static tables.
Categorization	The types of adaptive routing algorithm, are Centralized, isolation and distributed algorithm.	The types of Non Adaptive routing algorithm are flooding and random walks.
Complexity	Adaptive Routing algorithms are more complex.	Non-Adaptive Routing algorithms are simple.

Distance Vector Routing Algorithm

• The Distance vector algorithm is iterative, asynchronous and distributed.
  • Distributed: It is distributed in that each node receives information from one or more of its directly attached neighbors, performs calculation and then distributes the result back to its neighbors.
  • Iterative: It is iterative in that its process continues until no more information is available to be exchanged between neighbors.
  • Asynchronous: It does not require that all of its nodes operate in the lock step with each other.
• The Distance vector algorithm is a dynamic algorithm.
• It is mainly used in ARPANET, and RIP.
• Each router maintains a distance table known as Vector.

Three Keys to understand the working of Distance Vector Routing Algorithm:

• Knowledge about the whole network: Each router shares its knowledge through the entire network. The Router sends its collected knowledge about the network to its neighbors.
• Routing only to neighbors: The router sends its knowledge about the network to only those routers which have direct links. The router sends whatever it has about the network through the ports. The information is received by the router and uses the information to update its own routing table.
• Information sharing at regular intervals: Within 30 seconds, the router sends the information to the neighboring routers.

Distance Vector Routing Algorithm

Let d_x(y) be the cost of the least-cost path from node x to node y. The least costs are related by Bellman-Ford equation,

dx(y) = minv{c(x,v) + dv(y)}

Where the minv is the equation taken for all x neighbors. After traveling from x to v, if we consider the least-cost path from v to y, the path cost will be c(x,v)+d_v(y). The least cost from x to y is the minimum of c(x,v)+d_v(y) taken over all neighbors.

With the Distance Vector Routing algorithm, the node x contains the following routing information:

• For each neighbor v, the cost c(x,v) is the path cost from x to directly attached neighbor, v.
• The distance vector x, i.e., D_x = [ D_x(y) : y in N ], containing its cost to all destinations, y, in N.
• The distance vector of each of its neighbors, i.e., D_v = [ D_v(y) : y in N ] for each neighbor v of x.

Distance vector routing is an asynchronous algorithm in which node x sends the copy of its distance vector to all its neighbors. When node x receives the new distance vector from one of its neighboring vector, v, it saves the distance vector of v and uses the Bellman-Ford equation to update its own distance vector. The equation is given below:

dx(y) = minv{ c(x,v) + dv(y)}     for each node y in N

The node x has updated its own distance vector table by using the above equation and sends its updated table to all its neighbors so that they can update their own distance vectors.

Algorithm

At each node x,
Initialization

for all destinations y in N:
Dx(y) = c(x,y)     // If y is not a neighbor then c(x,y) = ∞
for each neighbor w
Dw(y) = ?     for all destination y in N.
for each neighbor w
send distance vector Dx = [ Dx(y)  : y in N ] to w
loop
  wait(until I receive any distance vector from some neighbor w)
  for each y in N:
  Dx(y) = minv{c(x,v)+Dv(y)}
If Dx(y) is changed for any destination y
Send distance vector Dx = [ Dx(y) : y in N ] to all neighbors
forever

Note: In Distance vector algorithm, node x update its table when it either see any cost change in one directly linked nodes or receives any vector update from some neighbor.

Let's understand through an example:

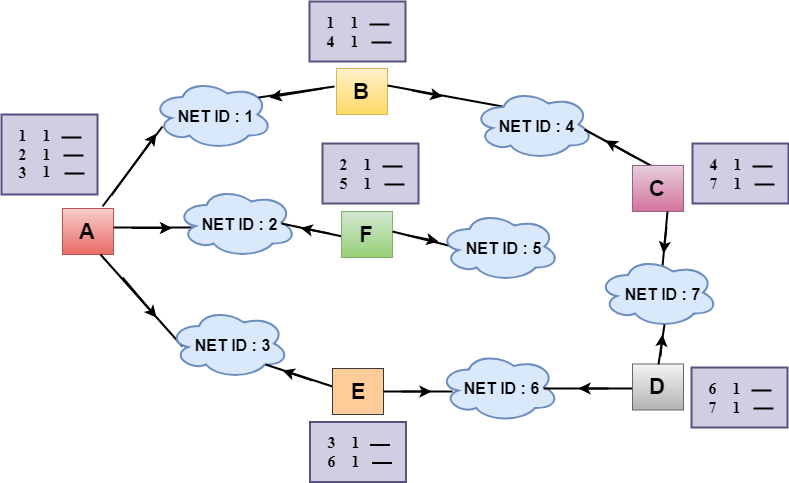
Sharing Information

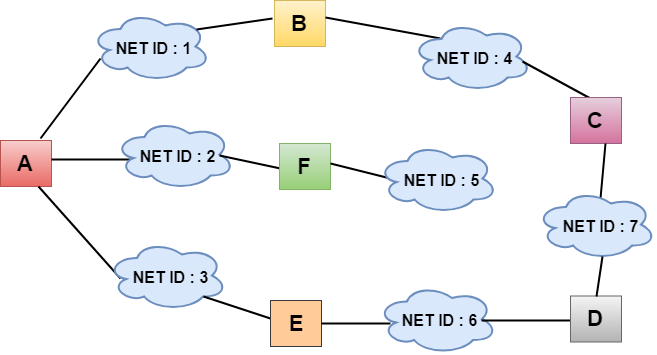
• In the above figure, each cloud represents the network, and the number inside the cloud represents the network ID.
• All the LANs are connected by routers, and they are represented in boxes labeled as A, B, C, D, E, F.
• Distance vector routing algorithm simplifies the routing process by assuming the cost of every link is one unit. Therefore, the efficiency of transmission can be measured by the number of links to reach the destination.
• In Distance vector routing, the cost is based on hop count.

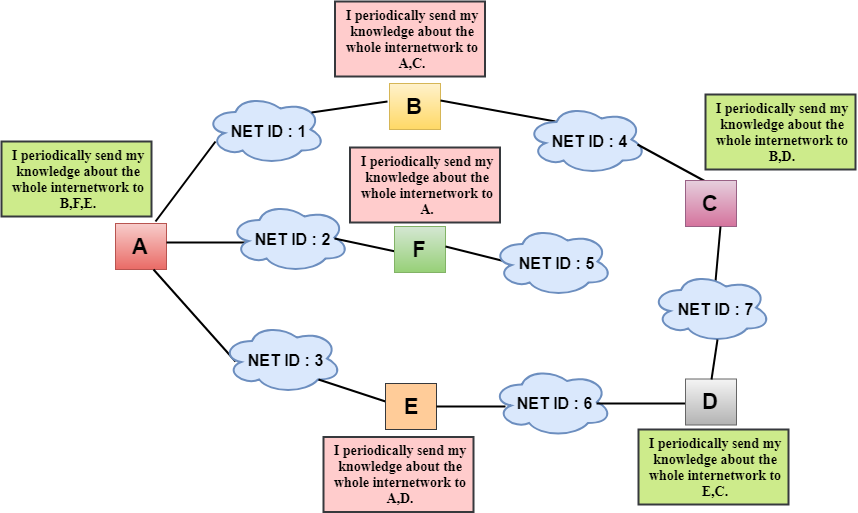
In the above figure, we observe that the router sends the knowledge to the immediate neighbors. The neighbors add this knowledge to their own knowledge and sends the updated table to their own neighbors. In this way, routers get its own information plus the new information about the neighbors.

Routing Table

Two process occurs:

• Creating the Table
• Updating the Table

Creating the Table

Initially, the routing table is created for each router that contains atleast three types of information such as Network ID, the cost and the next hop.

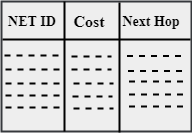
• NET ID: The Network ID defines the final destination of the packet.
• Cost: The cost is the number of hops that packet must take to get there.
• Next hop: It is the router to which the packet must be delivered.

• In the above figure, the original routing tables are shown of all the routers. In a routing table, the first column represents the network ID, the second column represents the cost of the link, and the third column is empty.
• These routing tables are sent to all the neighbors.

For Example:

A sends its routing table to B, F & E.  

B sends its routing table to A & C.  

C sends its routing table to B & D.  

D sends its routing table to E & C.  

E sends its routing table to A & D.  

F sends its routing table to A. 

Updating the Table

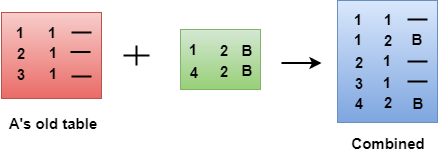
• When A receives a routing table from B, then it uses its information to update the table.
• The routing table of B shows how the packets can move to the networks 1 and 4.
• The B is a neighbor to the A router, the packets from A to B can reach in one hop. So, 1 is added to all the costs given in the B's table and the sum will be the cost to reach a particular network.

• After adjustment, A then combines this table with its own table to create a combined table.

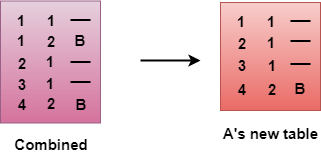
• The combined table may contain some duplicate data. In the above figure, the combined table of router A contains the duplicate data, so it keeps only those data which has the lowest cost. For example, A can send the data to network 1 in two ways. The first, which uses no next router, so it costs one hop. The second requires two hops (A to B, then B to Network 1). The first option has the lowest cost, therefore it is kept and the second one is dropped.

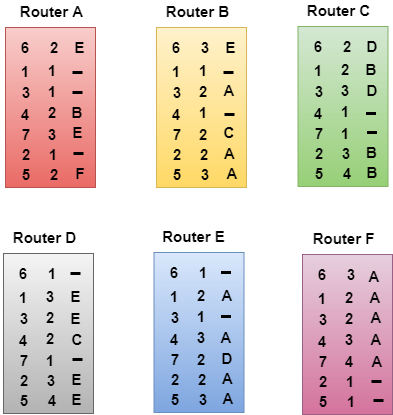
• The process of creating the routing table continues for all routers. Every router receives the information from the neighbors, and update the routing table.

Final routing tables of all the routers are given below:

Link State Routing

Link state routing is a technique in which each router shares the knowledge of its neighborhood with every other router in the internetwork.

The three keys to understand the Link State Routing algorithm:

• Knowledge about the neighborhood: Instead of sending its routing table, a router sends the information about its neighborhood only. A router broadcast its identities and cost of the directly attached links to other routers.
• Flooding: Each router sends the information to every other router on the internetwork except its neighbors. This process is known as Flooding. Every router that receives the packet sends the copies to all its neighbors. Finally, each and every router receives a copy of the same information.
• Information sharing: A router sends the information to every other router only when the change occurs in the information.

Link State Routing has two phases:

Reliable Flooding

• Initial state: Each node knows the cost of its neighbors.
• Final state: Each node knows the entire graph.

Route Calculation

Each node uses Dijkstra's algorithm on the graph to calculate the optimal routes to all nodes.

• The Link state routing algorithm is also known as Dijkstra's algorithm which is used to find the shortest path from one node to every other node in the network.
• The Dijkstra's algorithm is an iterative, and it has the property that after k^th iteration of the algorithm, the least cost paths are well known for k destination nodes.

Let's describe some notations:

• c( i , j): Link cost from node i to node j. If i and j nodes are not directly linked, then c(i , j) = ∞.
• D(v): It defines the cost of the path from source code to destination v that has the least cost currently.
• P(v): It defines the previous node (neighbor of v) along with current least cost path from source to v.
• N: It is the total number of nodes available in the network.

Algorithm

Initialization
N = {A}     // A is a root node.
for all nodes v
if v adjacent to A
then D(v) = c(A,v)
else D(v) = infinity
loop
find w not in N such that D(w) is a minimum.
Add w to N
Update D(v) for all v adjacent to w and not in N:
D(v) = min(D(v) , D(w) + c(w,v))

Until all nodes in N

In the above algorithm, an initialization step is followed by the loop. The number of times the loop is executed is equal to the total number of nodes available in the network.

Let's understand through an example:

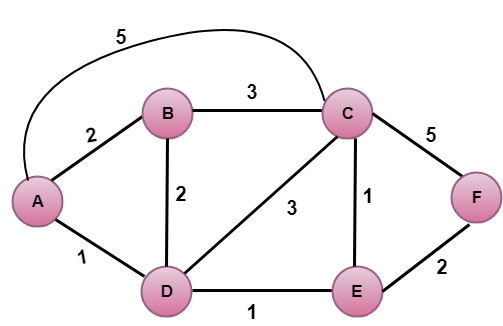
In the above figure, source vertex is A.

Step 1:

The first step is an initialization step. The currently known least cost path from A to its directly attached neighbors, B, C, D are 2,5,1 respectively. The cost from A to B is set to 2, from A to D is set to 1 and from A to C is set to 5. The cost from A to E and F are set to infinity as they are not directly linked to A.

Step	N	D(B),P(B)	D(C),P(C)	D(D),P(D)	D(E),P(E)	D(F),P(F)
1	A	2,A	5,A	1,A	∞	∞

Step 2:

In the above table, we observe that vertex D contains the least cost path in step 1. Therefore, it is added in N. Now, we need to determine a least-cost path through D vertex.

a) Calculating shortest path from A to B

v = B, w = D  

D(B) = min( D(B) , D(D) + c(D,B) )  

     = min( 2, 1+2)>  

     = min( 2, 3)  

The minimum value is 2. Therefore, the currently shortest path from A to B is 2.

b) Calculating shortest path from A to C

v = C, w = D  

D(B) = min( D(C) , D(D) + c(D,C) )  

     = min( 5, 1+3)  

     = min( 5, 4)  

The minimum value is 4. Therefore, the currently shortest path from A to C is 4.</p>

c) Calculating shortest path from A to E

v = E, w = D  

D(B) = min( D(E) , D(D) + c(D,E) )  

     = min( ∞,  1+1)  

     = min(∞, 2)  

The minimum value is 2. Therefore, the currently shortest path from A to E is 2.

Note: The vertex D has no direct link to vertex E. Therefore, the value of D(F) is infinity.

Step	N	D(B),P(B)	D(C),P(C)	D(D),P(D)	D(E),P(E)	D(F),P(F)
1	A	2,A	5,A	1,A	∞	∞
2	AD	2,A	4,D		2,D	∞

Step 3:

In the above table, we observe that both E and B have the least cost path in step 2. Let's consider the E vertex. Now, we determine the least cost path of remaining vertices through E.

a) Calculating the shortest path from A to B.

v = B, w = E  

D(B) = min( D(B) , D(E) + c(E,B) )  

     = min( 2 , 2+ ∞ )  

     = min( 2, ∞)  

The minimum value is 2. Therefore, the currently shortest path from A to B is 2.

b) Calculating the shortest path from A to C.

v = C, w = E  

D(B) = min( D(C) , D(E) + c(E,C) )  

     = min( 4 , 2+1 )  

     = min( 4,3)  

The minimum value is 3. Therefore, the currently shortest path from A to C is 3.

c) Calculating the shortest path from A to F.

v = F, w = E  

D(B) = min( D(F) , D(E) + c(E,F) )  

     = min( ∞ , 2+2 )  

     = min(∞ ,4)  

The minimum value is 4. Therefore, the currently shortest path from A to F is 4.

Step	N	D(B),P(B)	D(C),P(C)	D(D),P(D)	D(E),P(E)	D(F),P(F)
1	A	2,A	5,A	1,A	∞	∞
2	AD	2,A	4,D		2,D	∞
3	ADE	2,A	3,E			4,E

Step 4:

In the above table, we observe that B vertex has the least cost path in step 3. Therefore, it is added in N. Now, we determine the least cost path of remaining vertices through B.

a) Calculating the shortest path from A to C.

v = C, w = B  

D(B) = min( D(C) , D(B) + c(B,C) )  

     = min( 3 , 2+3 )  

     = min( 3,5)  

The minimum value is 3. Therefore, the currently shortest path from A to C is 3.

  

b) Calculating the shortest path from A to F.

v = F, w = B  

D(B) = min( D(F) , D(B) + c(B,F) )  

     = min( 4, ∞)  

     = min(4, ∞)  

The minimum value is 4. Therefore, the currently shortest path from A to F is 4.

Step	N	D(B),P(B)	D(C),P(C)	D(D),P(D)	D(E),P(E)	D(F),P(F)
1	A	2,A	5,A	1,A	∞	∞
2	AD	2,A	4,D		2,D	∞
3	ADE	2,A	3,E			4,E
4	ADEB		3,E			4,E

Step 5:

In the above table, we observe that C vertex has the least cost path in step 4. Therefore, it is added in N. Now, we determine the least cost path of remaining vertices through C.

a) Calculating the shortest path from A to F.

v = F, w = C  

D(B) = min( D(F) , D(C) + c(C,F) )  

     = min( 4, 3+5)  

     = min(4,8)  

The minimum value is 4. Therefore, the currently shortest path from A to F is 4.

Step	N	D(B),P(B)	D(C),P(C)	D(D),P(D)	D(E),P(E)	D(F),P(F)
1	A	2,A	5,A	1,A	∞	∞
2	AD	2,A	4,D		2,D	∞
3	ADE	2,A	3,E			4,E
4	ADEB		3,E			4,E
5	ADEBC					4,E

Final table:

Step	N	D(B),P(B)	D(C),P(C)	D(D),P(D)	D(E),P(E)	D(F),P(F)
1	A	2,A	5,A	1,A	∞	∞
2	AD	2,A	4,D		2,D	∞
3	ADE	2,A	3,E			4,E
4	ADEB		3,E			4,E
5	ADEBC					4,E
6	ADEBCF

Disadvantage:

Heavy traffic is created in Line state routing due to Flooding. Flooding can cause an infinite looping, this problem can be solved by using Time-to-leave field