Scan Converting a Straight Line

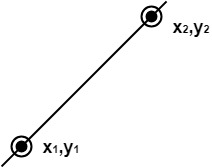
A straight line may be defined by two endpoints & an equation. In fig the two endpoints are described by (x₁,y₁) and (x₂,y₂). The equation of the line is used to determine the x, y coordinates of all the points that lie between these two endpoints.

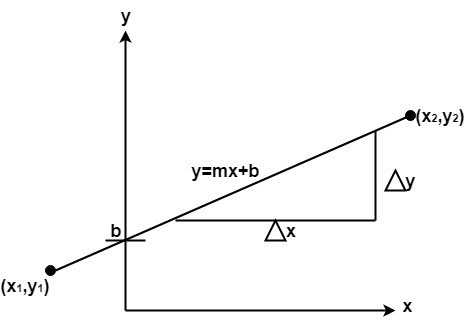
Using the equation of a straight line, y = mx + b where m = 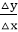 & b = the y interrupt, we can find values of y by incrementing x from x =x₁, to x = x₂. By scan-converting these calculated x, y values, we represent the line as a sequence of pixels.

Properties of Good Line Drawing Algorithm:

1. Line should appear Straight: We must appropriate the line by choosing addressable points close to it. If we choose well, the line will appear straight, if not, we shall produce crossed lines.

The lines must be generated parallel or at 45° to the x and y-axes. Other lines cause a problem: a line segment through it starts and finishes at addressable points, may happen to pass through no another addressable points in between.

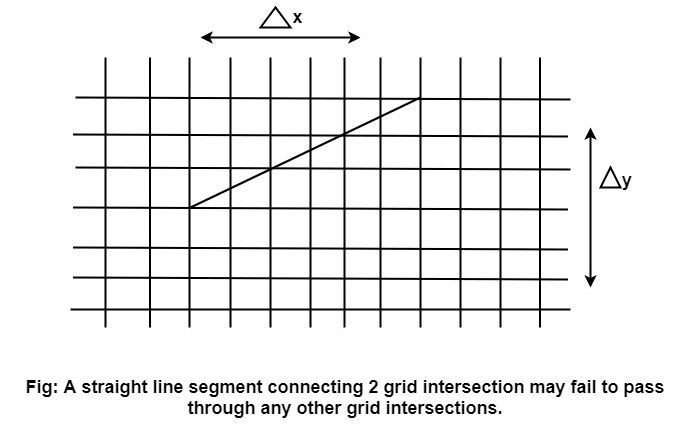
2. Lines should terminate accurately: Unless lines are plotted accurately, they may terminate at the wrong place.

3. Lines should have constant density: Line density is proportional to the no. of dots displayed divided by the length of the line.

To maintain constant density, dots should be equally spaced.

4. Line density should be independent of line length and angle: This can be done by computing an approximating line-length estimate and to use a line-generation algorithm that keeps line density constant to within the accuracy of this estimate.

5. Line should be drawn rapidly: This computation should be performed by special-purpose hardware.

Algorithm for line Drawing:

1. Direct use of line equation
2. DDA (Digital Differential Analyzer)
3. Bresenham's Algorithm

Direct use of line equation:

It is the simplest form of conversion. First of all scan P₁ and P₂ points. P₁ has co-ordinates (x₁',y₁') and (x₂' y₂' ).

Then       m = (y₂',y₁')/( x₂',x₁') and b =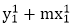 

If value of |m|≤1 for each integer value of x. But do not consider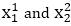 

If value of |m|>1 for each integer value of y. But do not consider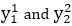 

Example: A line with starting point as (0, 0) and ending point (6, 18) is given. Calculate value of intermediate points and slope of line.

Solution: P₁ (0,0) P₇ (6,18)

              x₁=0
              y₁=0
              x₂=6
              y₂=18
              

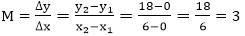
We know equation of line is
              y =m x + b
              y = 3x + b..............equation (1)

put value of x from initial point in equation (1), i.e., (0, 0) x =0, y=0
              0 = 3 x 0 + b
              0 = b ⟹ b=0

put b = 0 in equation (1)
              y = 3x + 0
              y = 3x

Now calculate intermediate points
    Let x = 1 ⟹ y = 3 x 1 ⟹ y = 3
    Let x = 2 ⟹ y = 3 x 2 ⟹ y = 6
    Let x = 3 ⟹ y = 3 x 3 ⟹ y = 9
    Let x = 4 ⟹ y = 3 x 4 ⟹ y = 12
    Let x = 5 ⟹ y = 3 x 5 ⟹ y = 15
    Let x = 6 ⟹ y = 3 x 6 ⟹ y = 18

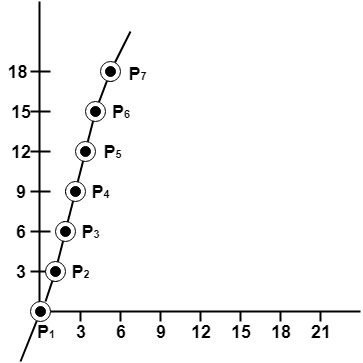
So points are P₁ (0,0)
              P₂ (1,3)
              P₃ (2,6)
              P₄ (3,9)
              P₅ (4,12)
              P₆ (5,15)
              P₇ (6,18)

Algorithm for drawing line using equation:

Step1: Start Algorithm

Step2: Declare variables x₁,x₂,y₁,y₂,dx,dy,m,b,

Step3: Enter values of x₁,x₂,y₁,y₂.
              The (x₁,y₁) are co-ordinates of a starting point of the line.
              The (x₂,y₂) are co-ordinates of a ending point of the line.

Step4: Calculate dx = x₂- x₁

Step5: Calculate dy = y₂-y₁

Step6: Calculate m =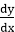 

Step7: Calculate b = y₁-m* x₁

Step8: Set (x, y) equal to starting point, i.e., lowest point and x_endequal to largest value of x.

              If dx < 0
                  then x = x₂
              y = y₂
                        x_end= x₁
        If dx > 0
              then x = x₁
                  y = y₁
                        x_end= x₂

Step9: Check whether the complete line has been drawn if x=x_end, stop

Step10: Plot a point at current (x, y) coordinates

Step11: Increment value of x, i.e., x = x+1

Step12: Compute next value of y from equation y = mx + b

Step13: Go to Step9.

Program to draw a line using LineSlope Method

#include <graphics.h>  
#include <stdlib.h>  
#include <math.h>  
#include <stdio.h>  
#include <conio.h>  
#include <iostream.h>  
  
class bresen  
{  
    float x, y, x1, y1, x2, y2, dx, dy, m, c, xend;  
    public:  
    void get ();  
    void cal ();  
};  
    void main ()  
    {  
    bresen b;  
    b.get ();  
    b.cal ();  
    getch ();  
   }  
    Void bresen :: get ()  
   {  
    print ("Enter start & end points");  
    print ("enter x1, y1, x2, y2");  
    scanf ("%f%f%f%f",sx1, sx2, sx3, sx4)  
}  
void bresen ::cal ()  
{  
    /* request auto detection */  
    int gdriver = DETECT,gmode, errorcode;  
    /* initialize graphics and local variables */  
    initgraph (&gdriver, &gmode, " ");  
    /* read result of initialization */  
    errorcode = graphresult ();  
    if (errorcode ! = grOK)    /*an error occurred */  
    {  
        printf("Graphics error: %s \n", grapherrormsg (errorcode);  
        printf ("Press any key to halt:");  
        getch ();  
        exit (1); /* terminate with an error code */  
    }  
    dx = x2-x1;  
    dy=y2-2y1;  
    m = dy/dx;  
    c = y1 - (m * x1);  
    if (dx<0)  
    {  
        x=x2;  
        y=y2;  
        xend=x1;  
    }  
    else  
    {  
        x=x1;  
        y=y1;  
        xend=x2;  
    }  
while (x<=xend)  
    {  
        putpixel (x, y, RED);  
        y++;  
        y=(x*x) +c;  
    }  
}

  

OUTPUT:

Enter Starting and End Points
Enter (X1, Y1, X2, Y2) 200 100 300 200