CIRCUIT SAT

According to given decision-based NP problem, you can design the CIRCUIT and verify a given mentioned output also within the P time. The CIRCUIT is provided below:-

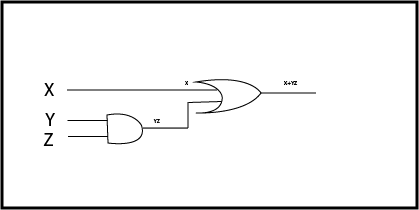
Note:- You can design a circuit and verified the mentioned output within Polynomial time but remember you can never predict the number of gates which produces the high output against the set of inputs/high inputs within a polynomial time. So you verified the production and conversion had been done within polynomial time. So you are in NPC.

SAT (Satisfiability):-

A Boolean function is said to be SAT if the output for the given value of the input is true/high/1

F=X+YZ (Created a Boolean function by CIRCUIT SAT)

These points you have to be performed for NPC

1. CONCEPTS OF SAT
2. CIRCUIT SAT≤ρ SAT
3. SAT≤ρ CIRCUIT SAT
4. SAT ϵ NPC

1. CONCEPT: - A Boolean function is said to be SAT if the output for the given value of the input is true/high/1.
2. CIRCUIT SAT≤ρ SAT: - In this conversion, you have to convert CIRCUIT SAT into SAT within the polynomial time as we did it
3. SAT≤ρ CIRCUIT SAT: - For the sake of verification of an output you have to convert SAT into CIRCUIT SAT within the polynomial time, and through the CIRCUIT SAT you can get the verification of an output successfully
4. SAT ϵ NPC: - As you know very well, you can get the SAT through CIRCUIT SAT that comes from NP.

Proof of NPC: - Reduction has been successfully made within the polynomial time from CIRCUIT SAT TO SAT. Output has also been verified within the polynomial time as you did in the above conversation.

So concluded that SAT ϵ NPC.